大学物理 磁介质

Chapter 7 - 磁场中的磁介质

原子与分子的磁矩

对于经典模型的电子来说，其存在轨道磁矩和自旋磁矩两种，其轨道磁矩大小为：

$$m = IS = e\cdot\frac{v}{2\pi r}\cdot \pi r^2 = \frac{evr}{2}$$

根据电子带负电不难得出，其与轨道角动量 $\overrightarrow{L}$ 之间满足：

$$\vec{m} = -\frac{e}{2m_e}\overrightarrow{L}$$

电子的自旋磁矩与自旋角动量 $\overrightarrow{S}$ 之间满足：

$$\vec{m} = -\frac{e}{m_e}\overrightarrow{S}$$

对于质子和中子，容易得出，质子轨道磁矩表达式与电子的仅相差一个负号，而中子无轨道磁矩

其自旋磁矩为：

$$\vec{m} = g\frac{e}{2m_p}\overrightarrow{S}$$

其中 $g$ 因子是粒子的固有属性

原子核、分子的磁矩是构成其的质子、中子与电子的磁矩之和

在外磁场中，粒子还会因为拉莫尔进动而产生感生磁矩，方向与原磁场相反

分子电流模型

将分子的磁矩等效于分子电流，分子电流的取向是否有序决定了宏观上物质是否显示出磁性

磁介质的磁化

保持传导电流 $I_0$ 不变，在长直密绕螺线管内充满均匀各向同性磁介质后，管内磁场变为：

$$\overrightarrow{B} = \mu_r \overrightarrow{B}_0$$

其中 $\mu_r$ 是相对磁导率

对于顺磁质，即 $\mu_r \approx 1^{+}$，其分子有固有磁矩，因此感生磁矩可忽略，在外磁场作用下，固有磁矩尽可能沿外磁场方向（有分子热运动），显示出微弱的顺磁性

对于逆磁质，即 $\mu_r \approx 1^{-}$，其分子没有固有磁矩，在外磁场作用下，感生磁矩与外磁场方向相反，显示出微弱的逆磁性

磁化强度

定义磁化强度矢量为，单位体积中分子磁矩的矢量和，即：

$$\overrightarrow{M} = \frac{\sum\vec{m}}{\Delta V}$$

$\Delta V$ 宏观上远小于介质的非均匀尺度，但是微观上远大于分子间距

实验表明，对于各向同性线性磁介质，满足：

$$\overrightarrow{M} = \frac{1}{\mu_0}\cdot\frac{\chi_m}{1 + \chi_m}\overrightarrow{B} = \frac{\mu_r - 1}{\mu_r\mu_0}\overrightarrow{B}$$

其中 $\chi_m = \mu_r - 1$ 称为磁化率

不适用于铁介质，即 $\mu_r >> 1$

磁化电流

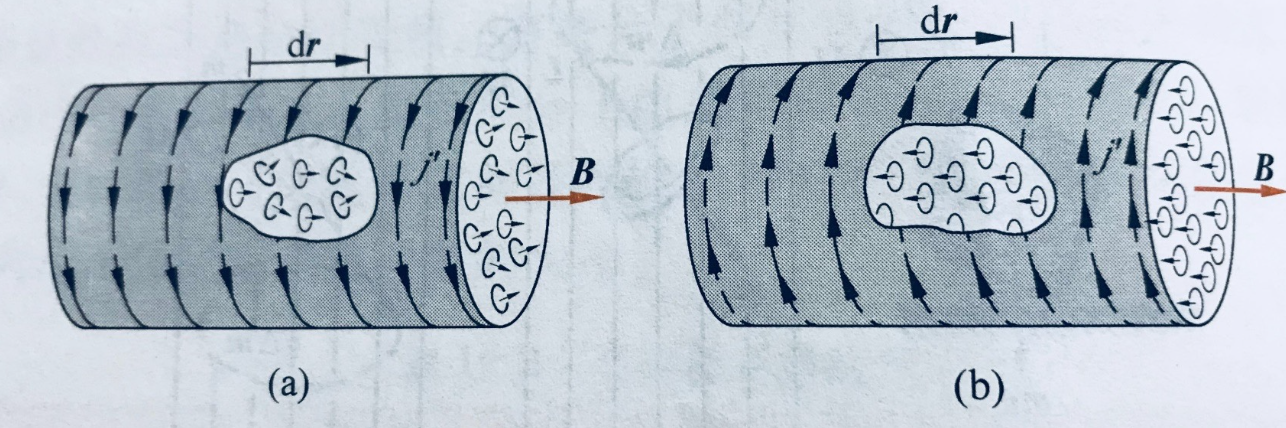
在外磁场中，顺磁 / 抗磁介质与圆电流产生的感生磁矩与外磁场方向相同 / 相反；但是表面上有小的圆电流未被抵消，总体效果为表面上有一层电流流过；该电流被称为束缚电流或磁化电流

顺磁质与抗磁质的磁化电流示意图

定量分析

穿过以 $L$ 为边界的任一曲面 $S$（$L$ 和 $S$ 成右手关系）的磁化电流为：

$$I' = \oint_L \overrightarrow{M}\cdot \mathrm{d}\,\vec{l}$$

根据 stokes 公式有：

$$\vec{j}' = \nabla \times \overrightarrow{M}$$

在介质表面，可以证明面电流密度为：

$$\vec{i} = \overrightarrow{M} \times \vec{e}_n$$

有磁介质时磁场规律

高斯定理与安培环路定理仍然成立，但是由于磁场是由传导电流和磁化电流共同形成，因此直接使用并不方便（类似电场），进行修正：

$$\oint_L\overrightarrow{B}\cdot\mathrm{d}\vec{l} = \mu_0 \left(I' + \sum I_0 \right) = \mu_0 \left(\oint_L \overrightarrow{M}\cdot \mathrm{d}\,\vec{l} + \sum I_0 \right)$$

化简得到：

$$\oint_L\left(\frac{\overrightarrow{B}}{\mu_0} - \overrightarrow{M} \right)\cdot \mathrm{d}\,\vec{l} = \sum I_0$$

定义磁场强度为：

$$\overrightarrow{H} = \frac{\overrightarrow{B}}{\mu_0} - \overrightarrow{M}$$

得到 $\overrightarrow{H}$ 的环路定理：

$$\oint_L\overrightarrow{H}\cdot \mathrm{d}\,\vec{l} = \sum I_0$$

根据 stokes 定理有：

磁化强度有自己的单位奥斯特 $\rm Oe$，满足：

$$1\,\,\mathrm{Oe} = \frac{10^3}{4\pi}\rm A/m$$

类似电场，对于各向同性线性磁介质，可以得到磁场强度、磁化强度、磁感应强度之间的关系：

$$\begin{align*} \overrightarrow{B} &= \mu_0\mu_r \overrightarrow{H} = \mu\overrightarrow{H} \\ \overrightarrow{M} &= (\mu_r - 1)\overrightarrow{H} \end{align*}$$

其中 $\mu = \mu_0\mu_r$ 称为磁导率

据此可以证明：对均匀各向同性介质，不论其磁化是否均匀，体内传导电流为零处，磁化电流必然为零

磁场的界面关系

1. 法向关系：

$$\left(\overrightarrow{B}_1 - \overrightarrow{B_2}\right)\cdot \vec{e}_n = 0 \implies B_{1n} = B_{2n}$$

其中 $\vec{e}_n$ 由介质 2 指向介质 1

2. 切向关系：

$$\overrightarrow{H}_1 \cdot \vec{e}_t= \overrightarrow{H}_2 \cdot \vec{e}_t \implies H_{1t} = H_{2t}$$

其中 $\vec{e}_t$ 沿分界面切向

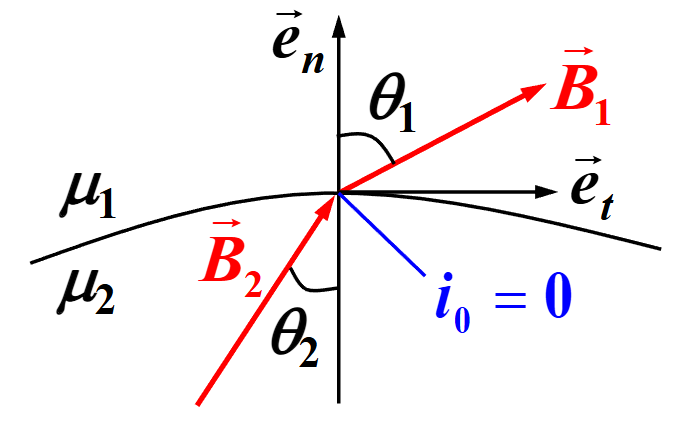
3. 对于各项同性介质，若 $i_0 = 0$，可以由几何关系得到：

$$\frac{\tan \theta_1}{\tan\theta_2} = \frac{\mu_1}{\mu_2}$$

电场线形成了类似光线的折射