大学物理 波粒二象性

Chapter D - 波粒二象性

黑体辐射

热辐射

我们把与温度有关的电磁辐射称为热辐射，热辐射波谱是连续谱，各种波长（频率）成份都有，但强度不同；当物体吸收的能量等于同一时间内辐射的能量时，物体温度恒定，此时称之为平衡热辐射

假设某温度为 $T$ 的物质在单位时间内，从单位表面发出的电磁波中，频率在 $\nu$ 附近 $\mathrm{d}\nu$ 间隔内的能量为 $\mathrm{d}E_\nu(T)$，则定义光谱辐出度为：

$$M_\nu(T) = \frac{\mathrm{d}E_\nu(T)}{\mathrm{d}\nu}$$

这个值实际表示了特定频率 $\nu$ 的辐射能量，因此总辐出度为：

$$M(T) = \int_0^\infty M_\nu(T)\mathrm{d}\nu$$

对于某一频率的光，我们定义单色吸收比是物质所能够吸收的能量占入射总能量的比例，即：

$$\alpha_\nu(T) = \frac{\mathrm{d}E_{\nu \text{ 吸收}}}{\mathrm{d}E_{\nu \text{ 入射}}} \in [0, 1]$$

黑体

如果某种物体可以能完全吸收各种波长电磁波而无反射，则称之为黑体，即 $\alpha_\nu = 1$

在一个温度为 $T$ 的孤立系统中，有一个黑体和 $n$ 个其他物质，如果此时系统处于平衡热辐射，则对于第 $i$ 个物体有：

$$\frac{M_{\nu i}}{\alpha_{\nu i}} = M_{\nu b}$$

其中 $M_{\nu b}$ 是黑体的辐出度

黑体辐射谱

我们可以通过实验装置，来测量同一温度下，某一黑体不同频率的光谱辐出度，得到 $M_\nu - \nu$ 曲线，这个曲线会是一个单峰曲线，假设其极值点为 $\nu_m$，在历史上，有很多对这个曲线的公式解释，例如：

• 维恩位移公式，给出了极值点的公式：

$$\nu_m = C_\nu T, \quad C_\nu = 5.880\times 10^{10} \,\,\rm Hz / K$$

• 斯特藩 - 玻耳兹曼定律，给出了计算总辐出度的方法，也即 $M_\nu - \nu$ 曲线下方的面积：

$$M(T) = \sigma T^4,\quad \sigma = 5.67\times 10^{-8} \,\,\rm W / m^2 \cdot K^4$$

• 维恩公式，在高频很准确，但是低频偏离：

$$M_\nu(T) = \alpha\nu^3e^{-\beta\nu / T}$$

• 瑞利 - 金斯公式，低频很准确，但是高频会发散：

$$M_\nu(T) = \frac{2\pi\nu^2}{c^2}kT$$

普朗克黑体辐射公式

普朗克假设频率为 $\nu$ 的简谐振子能量是离散的，能量子为：

$$\varepsilon = h\nu$$

得到的公式为：

其中 $h$ 是普朗克常数，一般取：

$$h \approx 6.63\times 10^{-34} \,\,\rm J\cdot s$$

光的二象性

光电效应

指的是光照射某些金属时，能从表面释放出电子的效应

• 当光的频率 $\nu$ 一定的时候，饱和光电流与光强成正比，即 $i_m \propto I$
• 当反向电压高于某一个值的时候，无法产生光电效应，这个值被称为截止电压 $U_c$，实验测得其满足：$U_c = K\nu - U_0$
• 当 $U_c \leq 0$ 即 $\nu \leq K / U_0$ 的时候，无需增加反向电压就无法产生光电效应，这个频率被称为极限频率

爱因斯坦光子理论

爱因斯坦将光也量子化，单个光子频率为 $\nu$ 的时候能量为 $\varepsilon = h\nu$

因此截止电压可以通过下述式子来计算：

$$eU_c = h\nu - A \implies U_c = \frac{h}{e}\nu - \frac{A}{e}$$

其中 $A$ 是金属的逸出功，计算结果与实验规律符合，并且这套理论能很好的解释实验现象

光的二象性特征

通过以下式子统一：

作为电磁波，光在空间弥散而连续；而作为粒子，光在空间中集中而分立；因此可以统一的用概率波来描述

具体来说，光子在某处出现的概率与该处的光强正相关

康普顿散射

康普顿散射现象是指：波长为 $\lambda_0$ 的高频电磁波（如X射线或伽马射线）在入射某一种物质后，散射光中会出现 $\lambda \neq \lambda_0$ 的现象，这与经典理论相悖

实验中还观察到：

• $\lambda$ 只与散射角 $\varphi$ 有关，并且 $\varphi$ 越大 $\lambda$ 越大
• $\varphi$ 增大会导致 $\lambda_0$ 的谱线强度降低

实验测得，散射波波长偏移：

$$\lambda - \lambda_0 = \Delta\lambda = \lambda_C(1 - \cos\varphi) = 2\lambda_C\sin^2\dfrac{\varphi}{2}$$

其中 $\lambda_C$ 是电子的康普顿波长，为常数，值约为 $2.41\times 10^{-3}\rm nm$

理论解释

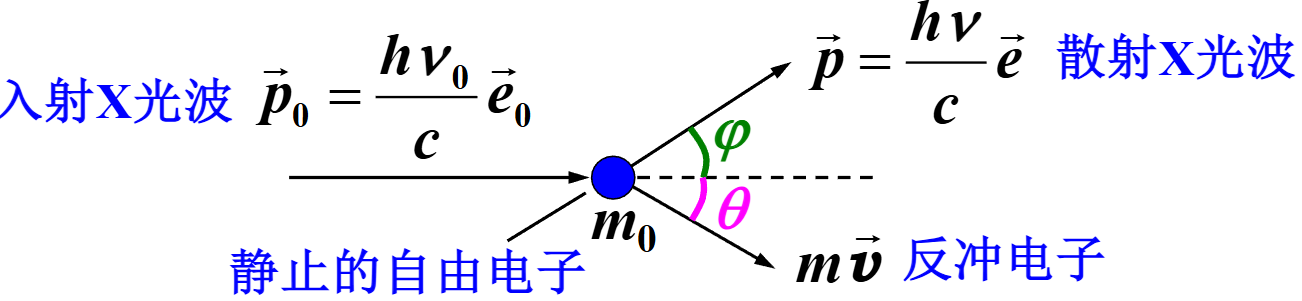
X 射线中的光子与物质中静止的自由电子碰撞，导致能量降低，因此频率降低，波长变大

将这个模型简化为弹性碰撞，利用能量守恒、动量守恒、相对论效应可以得到：

$$\lambda_C = \frac{h}{m_0c}$$

证明过程

简化后建模示意图

由能量守恒：$$h\nu_0 + m_0c^2 = h\nu + mc^2$$由动量守恒：$$\begin{align*} \frac{h\nu}{c}\cos\varphi + m&v\cos\theta = \frac{h\nu_0}{c} \\ \frac{h\nu}{c}\sin\varphi &= mv\sin\theta\end{align*}$$由洛伦兹变化有：$$m = \frac{m_0}{\sqrt{1 - v^2/c^2}}$$分离 $\theta$ 和 $\varphi$ 之后，将动量守恒的两组式子做变换得到：$$(h\nu)^2 + (h\nu_0)^2 - 2h^2\nu\nu_0\cos\varphi = m^2v^2c^2$$代入洛伦兹变换，消掉 $v$：$$(h\nu)^2 + (h\nu_0)^2 - 2h^2\nu\nu_0\cos\varphi = m^2c^4 \left(1 - \left(\frac{m_0}{m}\right)^2\right) = (m^2 - m_0^2)c^4$$对于能量守恒的式子，分离后变换得到：$$(h\nu)^2 + (h\nu_0)^2 - 2h^2\nu\nu_0 = (m - m_0)^2c^4$$上述两式相减：$$\begin{align*}h^2\nu\nu_0(1 - \cos\varphi) &= (m - m_0)m_0c^4 \\&= (m - m_0)c^2\cdot m_0c^2 \\&= h(\nu_0 - \nu)\cdot m_0c^2\end{align*}$$得到：$$\Delta\lambda = \frac{c}{\nu} - \frac{c}{\nu_0} = \frac{c(\nu_0 - \nu)}{\nu_0\nu} = \frac{h}{m_0c}(1 - \cos\varphi)$$证毕

其中 $m_0$ 是电子的静质量

实物粒子的波动性

一个能量为 $E$、动量为 $p$ 的实物粒子，同时也具有波动性。它的波长 $\lambda$、频率 $\nu$ 和 $E, p$ 的关系与光子的情形一样：

$$E = h\nu,\quad p = \dfrac{h}{\lambda}$$

这里的波长被称为德布罗意波长

物质波通过电子在晶体上的衍射实验得到了证实，当电子的波长满足晶体的布拉格条件时，将能够观察到电流的极大值

假设加速电压为 $U$，则布拉格条件为：

$$2d\sin\varphi = k\lambda = \frac{kh}{p} = \frac{kh}{\sqrt{2emU}}$$

这说明 $I - \sqrt{U}$ 曲线应该出现等距的峰值

当然也可以通过其他衍射实验证实

物质波理论

一般的宏观物体物质波波长极小，因此只表现出粒子性

并且对于一般的宏观粒子，假设其物质波波速为 $u$，运动速度为 $v$，则有：

$$u = \lambda\nu = \frac{h}{p}\cdot\frac{E}{h} = \frac{mc^2}{mv} = \frac{c^2}{v} \implies\boxed{uv = c^2}$$

一般情况下，求波长可以利用相对论能量关系：

$$E^2 = E_0^2 + p^2c^2$$

即：

$$\lambda = \frac{h}{p} = \frac{hc}{\sqrt{E^2 - E_0^2}} = \frac{hc}{E_k^2 + 2E_kE_0}$$

概率波

玻恩表示，德布罗意波并不像经典波那样代表实在的物理量的波动，而是描述粒子在空间概率分布的“概率波”

假设三维空间中，概率波波函数为 $\Psi(\vec{r}, t)$，这是一个复函数，其本身的值没有物理意义，但是模方表示了在 $t$ 时刻 $\vec{r}$ 端点处，单位体积内一个例子出现的概率，则 $\mathrm{d}V$ 体积内出现粒子的概率为：

$$|\Psi(\vec{r}, t)|^2\mathrm{d}V$$

这从统计上要求了：

• 有限体积中粒子出现的概率必须是有限值：

$$\iiint\limits_{\Delta V}|\Psi(\vec{r}, t)|^2\mathrm{d}V <+\infty$$

• 全空间 $\Omega$ 中粒子出现的概率一定是 $1$：

$$\iiint\limits_{\Omega}|\Psi(\vec{r}, t)|^2\mathrm{d}V = 1$$

• $\Psi(\vec{r}, t)$ 应该是单值函数
• 势场性质和边界条件要求 $\Psi(\vec{r}, t)$ 及其一阶导数（反映概率流）是连续的

微观粒子的波动性，实质上就是概率幅 $\Psi$ 的相干叠加

态叠加原理

设粒子可处于一系列互异的、独立的状态中的任何一个状态，状态集为 $\{\Psi_i\}_{i = 1}^n$，则任意若干状态的线性叠加也是粒子的一个可能状态：

$$\Psi = \sum_k C_k\Psi_k, \quad C_k \in \mathbb{C}$$

其中 $|C_k|^2$ 表示处于 $\Psi_k$ 状态的概率

自由粒子波函数

自由粒子的德布罗意波是单色平面波

经典一维单色平面波波函数为：

$$y(x, t) = Ae^{-i(\omega t - kx)}$$

将其中的波动参数换为粒子参数，即利用：

$$\omega = 2\pi\nu = \frac{2\pi E}{h},\quad k = \frac{2\pi}{\lambda} = \frac{2\pi p}{h}$$

定义约化普朗克常数为：

$$\hbar = \frac{h}{2\pi} \approx 1.05\times 10^{-34}\,\,\mathrm{J\cdot s} = 6.58\times10^{-16}\,\,\rm eV\cdot s$$

则自由粒子波函数为：

$$\Psi(x, t) = Ae^{\frac{i}{\hbar}(px - Et)} = Ae^{\frac{i}{\hbar}px}e^{-\frac{i}{\hbar}Et} = \Phi(x)e^{-\frac{i}{\hbar}Et}$$

其中 $\Phi(x) = Ae^{\frac{i}{\hbar}px}$ 是空间波函数

扩展到三维空间：

$$\Phi(\vec{r}) = Ae^{\frac{i}{\hbar}\vec{p}\cdot\vec{r}}$$

不确定性关系

不确定关系是微观粒子具有波粒二象性的必然结果，表现为：在同一方向上，粒子的坐标和动量不能同时确定

即：

$$\Delta x\cdot\Delta p_x \geq \frac{\hbar}{2},\quad\Delta y\cdot\Delta p_y \geq \frac{\hbar}{2},\quad\Delta z\cdot\Delta p_z \geq \frac{\hbar}{2}$$

同样，有能量时间不确定性关系：

$$\Delta E\cdot\Delta t \geq \frac{\hbar}{2}$$

具有不确定性关系的一对物理量称为共轭物理量

其中，$\hbar$ 被称为约化普朗克常数，其值为：

$$\hbar = \frac{h}{2\pi}\approx 1.055 × 10^{-34} \rm\,\, J·s$$