大学物理 光的偏振

Chapter C - 光的偏振

光的偏振状态

由于光是横波，即传播方向与振动方向垂直，因此传播方向可以在一个平面内变化，也即有不同的振动状态，这就是偏振

这一章用矢量合成来理解会很简单！

完全偏振光

指的是光矢量（即电场矢量）的振动方式被完全限制在一种规则、确定的模式中，没有任何随机成分的光，主要分成线偏振光、圆偏振光和椭圆偏振光三种

1. 线偏振光：指各点光矢量的振动方向在同一平面内，可看成是由两束频率相同、传播方向相同、光矢量振动方向相互垂直、相位差为 0 或 $\pm\pi$ 的线偏振光的合成
2. 圆偏振光：指光矢量在波面内的端点轨迹是圆，可看成是由两束频率相同、传播方向相同、光矢量振动方向相互垂直、相位差为 $\pm\dfrac{\pi}{2}$ 的线偏振光的合成
3. 椭圆偏振光：指光矢量在波面内的端点轨迹是椭圆，可看成是由两束频率相同、传播方向相同、光矢量振动方向相互垂直、相位差固定的线偏振光的合成，当相位差为 $\pm\dfrac{\pi}{2}$ 的时候称为正椭圆偏振光，也即选取的椭圆轨迹的长短轴为坐标轴

线偏振光示意图

圆偏振光示意图

椭圆偏振光示意图

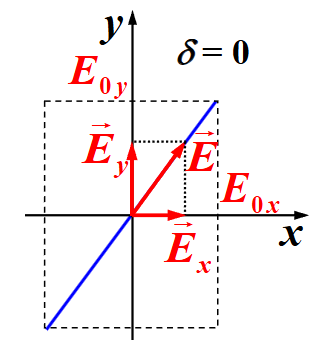
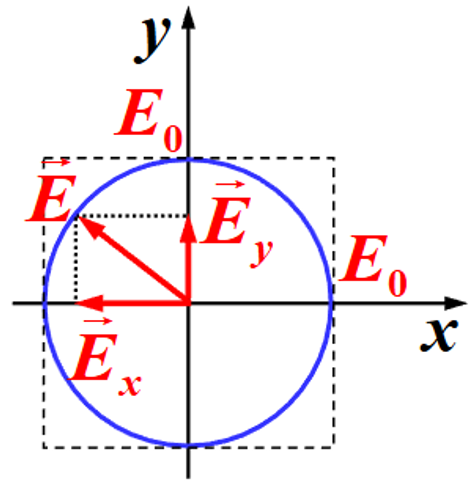
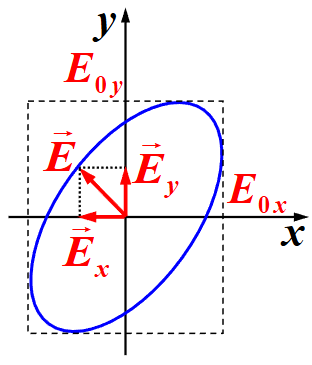
我们规定圆和椭圆偏振光的旋转方向为：面向光的传播方向，顺时针为右旋，逆时针为左旋

这样的话，线偏振光可以看成是两束频率相同、相位相同、振幅相同、传播方向相同的左、右旋圆偏振光的合成

非偏振光

对光场中每一点，光矢量在波面内的振动是方向随机、等幅的，振动没有优势方向，利用矢量正交分解的思想，可以证明非偏振光可分解为两振动方向相互垂直的、等幅的（强度相等）、不相干的线偏振光

自然光其实就是非偏振光，光源中大量的原子或分子独立、随机地发光。在垂直于传播方向的平面内，电场的振动方向在所有可能的方向上均匀分布，没有一个方向占优势

部分偏振光

由非偏振光和完全偏振光混合而成，在某些方向上振动较强，可以计算偏振度：

$$P = \frac{I_p}{I_t} = \frac{I_p}{I_p + I_n}$$

其中，$I_t$ 是部分偏振光的强度，$I_p$ 是其中完全偏振光的强度，$I_n$ 是其中自然光的强度

线偏振光的起偏与检偏

偏振片是一种光学器具，其只允许一个振动方向的光通过（这个方向被称为透振方向），通过偏振片可以得到线偏振光

将从自然光（非偏振光）中获得线偏振光的过程称为起偏；检查一束光是否是线偏振光、并确定其振动方向的过程称为检偏

检偏的原理是马吕斯定律：

因此，将起偏器得到的线偏振光打到另一个偏振片上，旋转这个偏振片，当观察到光强极弱，即消光时，即可得到线偏振光的方向与此时的透振方向垂直

以下是不同偏振类型的光通过检偏器后的光强变化

反射和折射光的偏振

非偏振光经过反射和折射后得到部分偏振光，将振动垂直于入射面的称为 S 分量，平行于入射面的称为 P 分量，则：

• 反射光 S 分量比例更大
• 折射光 P 分量比例更大
• 反射光与折射光的偏振度与入射角 $i$ 有关

当 $i$ 等于某个值 $i_0$ 的时候，反射光会变为完全偏振光，其中只包含 S 分量，设此时折射角为 $r_0$，则一定满足：

$$i_0 + r_0 = \frac{\pi}{2}$$

$i_0$ 被称为起偏角，也称为布儒斯特角，根据斯涅尔定理和上式可以推出布儒斯特定律：

这说明在布儒斯特角入射的情况下，只有垂直于入射面的分量会被反射，因此可以利用这个特性来区分偏振状态（自然光、线偏振光、部分偏振光）

考虑将入射光以 $i_0$ 入射到表面，以入射线为轴旋转光源，即改变入射光振动方向与入射面的夹角，则：

• 当反射光光强不变时：自然光
• 当光强会变化且出现消光时：线偏振
• 当光强变化但是不出现消光时：部分偏振

双折射现象

1 束光入射到各向异性介质内，产生 2 束折射光，我们将其分别称为：

• o 光：寻常光，遵循折射定律
• e 光：非寻常光，不遵循折射定律（折射率不是常数），也不一定在入射面内

实验观察可以证明，o 光和 e 光都是线偏振光，并且偏振方向相互垂直

当光在晶体内沿某个特殊方向传播时，不会发生双折射，这个方向被称为 光轴，晶体中光的传播方向与晶体光轴构成的平面叫该束光的主平面

主平面与两束光的振动方向

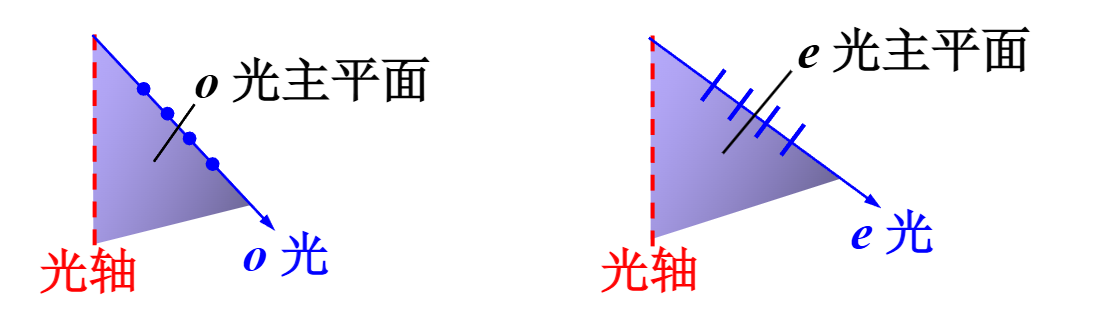
从图中可以看出，o 光振动垂直于主平面，而 e 光振动在主平面内

由于一般 e 光不在入射面内，因此光轴也不在入射面内，o 光和 e 光的主平面不重合；当光轴在入射面内时，入射面、两束折射光的主平面均重合

根据折射定律可以知道，o 光速度沿各个方向为常数，而 e 光速度不是，在光轴方向上，e 光速度和 o 光相同，而在垂直光轴方向上，e 光和 o 光的速度差别最大，设在垂直光轴方向上速度分别为 $v_e, v_o$，则折射率：

$$n_e = \frac{c}{v_e},\quad n_o = \frac{c}{v_o}$$

这两个折射率被称为主折射率，当 $n_o < n_e$ 时，晶体为正晶体，反之为负晶体

单轴晶体中光的传播

单轴晶体指的是只有一条光轴的晶体

假设在晶体内有一子波源 O，则根据各向异性，O 点会发出两组惠更斯子波，o 光各个方向速度相同，为球面波，e 光各个方向速度不同，为旋转椭球面波

由于光轴方向上，o 光和 e 光的速度相同，因此两波面在这个方向上相切，并且光轴是球面和旋转椭球面的旋转轴

晶体中的子波波阵面

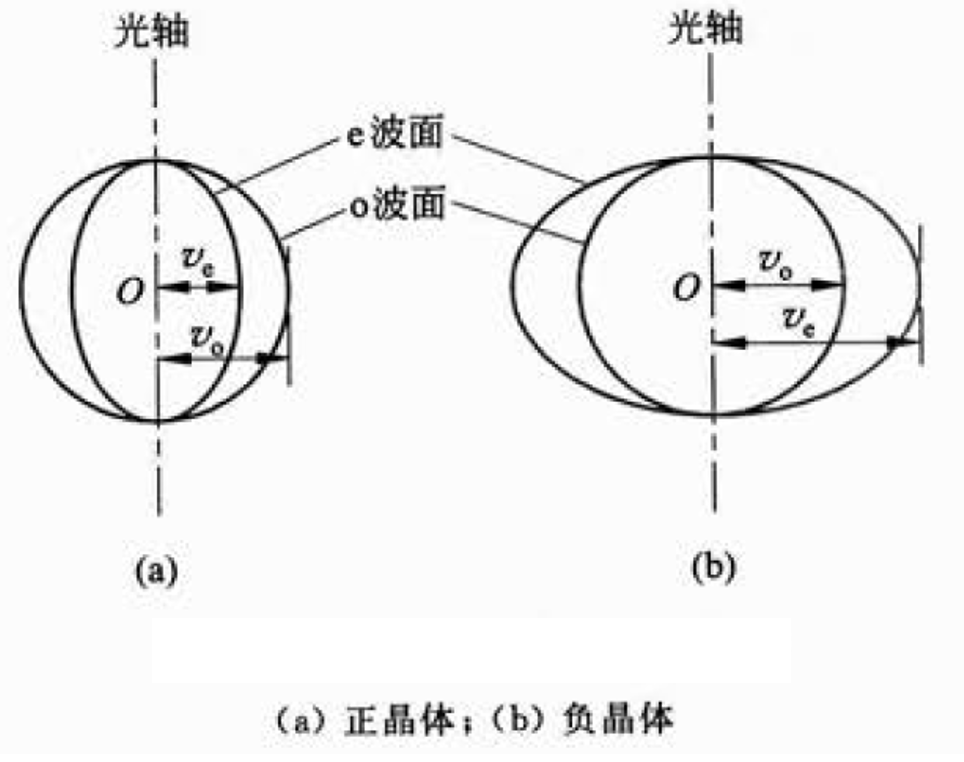
因此可以根据这个原理，绘制出不同方向光轴、不同方向入射光的情况下的 o 光和 e 光

不同情况下的 o 光和 e 光

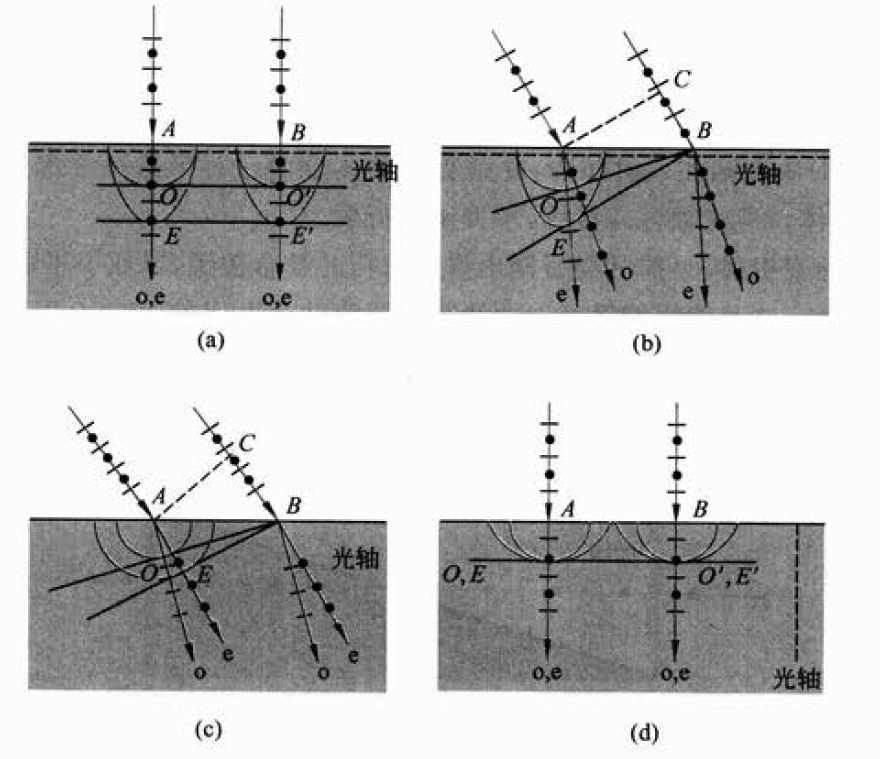
图中：

• (a) 为入射光垂直于晶面，光轴在入射面内，并且与晶面平行，由于此时 o 光和 e 光速度不同，因此也发生了双折射
• (b) 为入射光斜向射入，光轴在入射面内，并且与晶面平行
• (c) 为入射光斜向射入，光轴垂直于入射面，由于光轴是旋转对称轴，因此这种情况下 e 光也遵从折射定律
• (d) 为入射光垂直于晶面，光轴在入射面内，并且与晶面垂直，这种情况无双折射

椭圆偏振光与圆偏振光

我们将光轴平行于入射面的晶体薄片称之为晶片，当一束光正入射的时候，o 光和 e 光方向相同，但是由于主折射率不同，因此在晶体内两束折射光速度不同，即相位不同，相位差为：

$$|\Delta\varphi| = \frac{2\pi d}{\lambda}\cdot|n_o - n_e|$$

其中 $d$ 为晶片的厚度

当固定入射光波长 $\lambda$ 的时候，通过调整晶片材质和厚度可以让相位差为一些特殊值，从而让通过晶片后的光为椭圆偏振光或圆偏振光，这被称为波片

• 四分之一波片：$|n_o - n_e|d = \lambda / 4 \implies |\Delta\varphi| = \pi / 2$
• 二分之一波片：$|n_o - n_e|d = \lambda / 2 \implies |\Delta\varphi| = \pi$
• 全波片：$|n_o - n_e|d = \lambda \implies |\Delta\varphi| = 2\pi$

椭圆与圆偏振光的起偏

根据上图 (a) 中的图像可以知道，在正入射晶片的情况下，o 光的振动方向与与入射面垂直，而 e 光的振动方向在入射面内，平行于光轴

o 光和 e 光的振幅关系

上图中，光轴方向是 $y$ 轴，直线 P 是入射线偏振光的振动方向，与光轴的夹角为 $\alpha$，入射面为 $yOz$ 平面，则 o 光的振动方向是沿 $x$ 轴，e 光的振动方向是 $y$ 轴，

假设入射光的总振幅是 $A_\text{in}$，则容易得到：

$$A_o = A_\text{in}\sin\alpha,\quad A_e = A_\text{in}\cos\alpha$$

而出射光矢量在 o 轴和 e 轴（分别对应图中的 $x$ 轴和 $y$ 轴）上有 $|\Delta\varphi|$ 的相位差，对于四分之一波片来说，相位差为 $\dfrac{\pi}{2}$，因此：

• 当 $\alpha = 0$ 或 $\pi / 2$ 时，o 光或 e 光只保留一条，因此出射光只在一个方向上振动，还是线偏振
• 当 $\alpha = \pi / 4$ 时，$A_e = A_o$，这说明出射光由两个振幅相等、振动方向垂直、相位差为 $\pi / 2$ 的线偏振光合成，即为圆偏振光
• 当 $\alpha$ 为其他值的时候，同理得到的是正椭圆偏振光

可以总结完全偏振光经四分之一波片后的偏振态：

同理也可以分析出二分之一波片对偏振的影响，对于线偏振光来说，其出射光始终是线偏振光，并且振动面关于光轴镜面对称

椭圆与圆偏振光的起偏

由于值只使用偏振片的检偏器无法分辨自然光与圆偏振光、椭圆偏振光与部分偏振光AC，而这些光在通过四分之一波片后会有不同的行为，因此可以在检偏器之前加一个波片

• 自然光通过波片后仍为自然光，因此通过检偏器之后 $I$ 不变
• 圆偏振光通过波片后为线偏振光，因此通过检偏器之后 $I$ 会变化，并且会发生消光
• 正椭圆偏振光通过波片后为线偏振光，因此通过检偏器之后 $I$ 会变化，并且会发生消光
• 部分偏振光通过波片后仍然为部分偏振光（有自然光成分），因此通过检偏器之后一定不会发生消光

据此，可以区分出各种偏振类型的光

偏振光的干涉

偏振光干涉装置

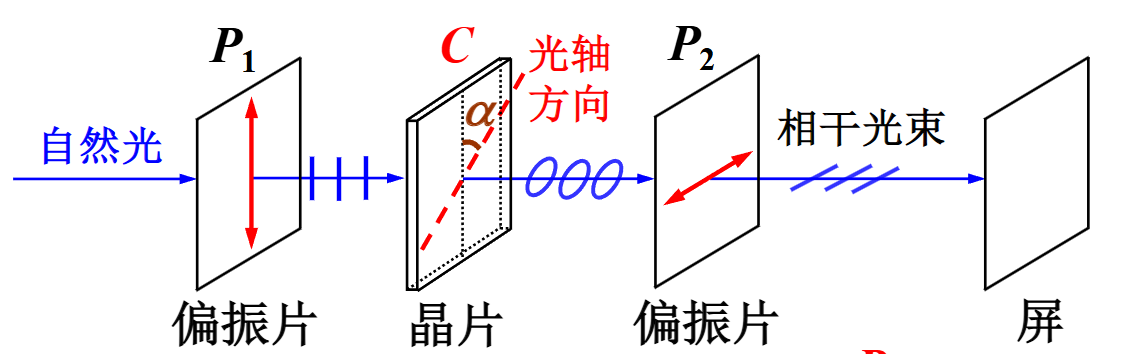
考虑上图所示的干涉装置，其中 $P_1, P_2$ 的偏振化方向正交

假设经过 $P_1$ 后，线偏振光的振幅是 $A_1$，则经过晶片后，振幅为：

$$A_o = A_1\sin\alpha, \quad A_e = A_1\cos\alpha$$

由于 e 光沿光轴，o 光垂直光轴，并且光轴与 $P_2$ 偏振化方向夹角为 $\dfrac{\pi}{2} - \alpha$，因此经过 $P_2$ 后：

$$A_{2o} = A_o\cos\alpha = A_1\sin\alpha\cos\alpha, \quad A_{2e} = A_e\sin\alpha = A_1\cos\alpha\sin\alpha$$

因此经过 $P_2$ 后两束光振幅相等

接下来讨论两束光的相位差

首先晶片会带来一个相位差：

$$|\Delta\varphi_C| = \frac{2\pi d}{\lambda}|n_o - n_e|$$

考虑上述的矢量分解过程：

1. 将 $\overrightarrow{A}_1$ 分解为沿光轴方向 $\overrightarrow{A}_e$ 和垂直光轴方向 $\overrightarrow{A}_o$
2. 将$\overrightarrow{A}_e$ 和 $\overrightarrow{A}_o$ 分别向 $P_2$ 方向上做投影

那由于光轴位于 $P_1, P_2$ 所形成的较小角之间，所以最终得到的两个向量应该是反向的，也即会有额外的 $\pi$ 的相位差，最终相位差是：

$$|\Delta\varphi| = \frac{2\pi d}{\lambda}|n_o - n_e| + \pi$$

因此得到相长干涉和相消干涉的条件：

$$\begin{align*} 相长\quad |\Delta\varphi| &= 2k\pi \implies d = \frac{2k - 1}{|n_o - n_e|}\frac{\lambda}{2} \\ 相消\quad |\Delta\varphi| &= (2k + 1)\pi \implies d = \frac{k\lambda}{|n_o - n_e|} \\ \end{align*}$$

因此，干涉现象为：

• 当晶片厚度均匀时：
  • 如果是单色光入射，则相位差固定，屏上亮度均匀，颜色与入射光颜色相同
  • 如果是白光入射，则由于某种光发生相消干涉，导致屏上呈现其互补色，亮度也均匀，这被称为色偏振
• 当晶片厚度不均匀时，如劈尖：
  • 单色光入射出现等厚条纹
  • 白光入射出现彩色条纹

旋光现象

旋光现象指的是，当线偏振光沿着光轴方向通过某种物质时，振动面会发生旋转，具体旋转角度为：

$$\theta = al$$

其中 $a$ 是旋光率，$l$ 是物质在光线传播方向上的厚度

面对光传播方向，使振动面产生逆（顺）时针转动的物质称为左（右）旋体

菲涅尔的解释

由于线偏振光可以看成是两束频率相同、相位相同、振幅相同、传播方向相同的左、右旋圆偏振光的合成，因此如果旋光物质对左右旋的圆偏振光折射率不同，则可以解释旋光现象

假设对左右旋圆偏振光的折射率分别为 $n_L, n_R$，则通过晶体后左旋光相位变化为：

$$\Delta\varphi_L = \omega_L\Delta t = 2\pi\nu\cdot\frac{l}{v_L} = \frac{2\pi ln_L}{c/\nu} = \frac{2\pi l}{\lambda}n_L$$

右旋光相位变化同理，因此相位差为：

$$|\Delta\varphi| = |\Delta\varphi_L - \Delta\varphi_R| = \frac{2\pi l}{\lambda}|n_L - n_R|$$

而偏振面旋转角为：

$$\theta = \left|\frac{\Delta\varphi_L + \Delta\varphi_R}{2} - \Delta\varphi_L\right| = \frac{1}{2}|\Delta\varphi| = \frac{\pi}{\lambda}|n_L - n_R|\cdot l$$

这说明旋光率为：