Chapter A - 光的干涉
光源的相干性
光源
光源的最基本发光单元是分子、原子,分为普通光源和激光光源两类
- 普通光源自发辐射,每个原子发光是间隙式的,不同次发出的光是独立的,不相干的
- 激光光源受激辐射,可以实现光放大,能产生单色性好(波列长大)、相干性好的光波
发光频率 ν=ΔE/h,定义波列长 L 是光源中一个原子或分子一次发光所持续发出的那一段有限长度的电磁波,则:
L=τ⋅c=Δλλ2
其中,τ 是一次发光的时间,λ 为中心波长,Δλ 是光源谱线宽度
第二个等号需要 Fourier 分析证明
光的相干性
对于两个发光点A,B,其距离空间任意一点 P 的距离分别为 r1,r2,则其在 P 点产生的场强大小为:
Ei=Ei0cos(ωt−kri+φi0)
其中:k=cω=λ2π
考虑振动方向平行,即场强同向,则合场强大小:
E=E1+E2=E0cos(ωt+φ)
其中 E0 是合成振幅,满足:
E02=E102+E202+2E10E20cosΔφ
相位差为:
Δφ=−k(r2−r1)+(φ20−φ10)
由于光强满足 I∝E2,因此:
I=I1+I2+2I1I2cosΔφ
其中最后一项被称为干涉项
cosΔφ 表示统计意义上取平均
- 非相干光源:满足 cosΔφ=0
- 完全相干光源:满足 cosΔφ=cosΔφ
- 相长干涉:Δφ=±2kπ
- 相消干涉:Δφ=±(2k+1)π
定义衬比度:
V=Imax+IminImax−Imin
衬比度表示了条纹的明暗程度
双缝干涉
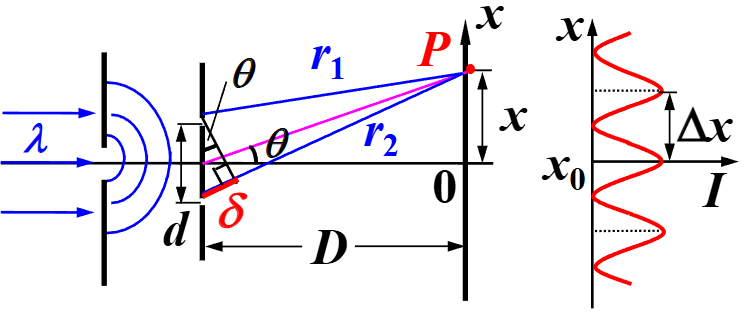
满足 λ<<d<<D,我认为图中有一处地方不准确,即粉色的线与板中心轴线形成的 θ,与 δ,d 所在的小直角三角形中标记出的 θ,并非严格相等,需要近似
则波程差为:
δ=r2−r1≈dsinθ≈dtanθ=d⋅Dx
相位差:
Δφ=δ⋅λ2π
因此,干涉出来的明暗条纹分别满足:
明纹δ=±kλ⟹x±k=±dkDλk∈N暗纹δ=±(k+21)λ⟹x±(k+1/2)=±(k+21)dDλ
因此,当 θ 不太大的时候,干涉条纹间距为:
Δx=dDλ
将不同明纹的下标称为明纹的级次,则白光入射时,0 级明纹中心为白色,可用来定 0 级位置,其余级明纹构成彩带,从第 2 级出现重叠
光强公式
在双缝干涉中,假设 I1=I2=I0,则可以化简为:
I=4I0cos22Δφ=4I0cos2λπδ=4I0cos2(λDxd⋅π)
时间相干性
准单色光
由于普通光源内部粒子发光不同步,因此其发光的时候并不能得到完全理想的单色光,而是在某个中心波长附近有一定波长范围的光,这被称为准单色光
准单色光的 I−λ 曲线为单峰曲线,设最高点为 i0,则 2i0 对应两个波长,这两个波长的差被称为谱线宽度 Δλ
则 λΔλ 越小,光的单色性越好
非单色性的影响
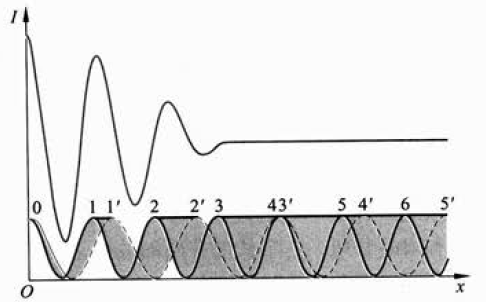
准单色光中,每一处不同波长的光产生的条纹会叠加(光强叠加),若在 x 处,波长最大的光和波长最小的光所产生的条纹,错位超过了一整个明纹间距,则此处,不同波长的光的相位集合包含了 [0,2π],因此不同波长的光在此处的光强恰好被均匀为相同的值,干涉条纹消失
如上图,阴影部分为所有波长的光 I−x 图像集合,实线为最小波长的干涉条纹,虚线为最大波长的干涉条纹,上部的曲线为合光强曲线
因此,最大相干能级应满足:
kM(λ+2Δλ)=(kM+1)(λ−2Δλ)
考虑 λ>>Δλ,解得:
kM=Δλλ
我们称两列波能发生干涉的最大波程差为相干长度,有:
δM=kMλ=Δλλ2
可以看出,δM=Lc
这是因为只有同一波列分成的两部分,经过不同路程再相遇时,才能发生干涉,也即波程差不能大于波列长
因此,可以根据波列长的定义,得到相干时间的计算式:
τ=cδM=cΔλλ2
空间相干性
极限宽度
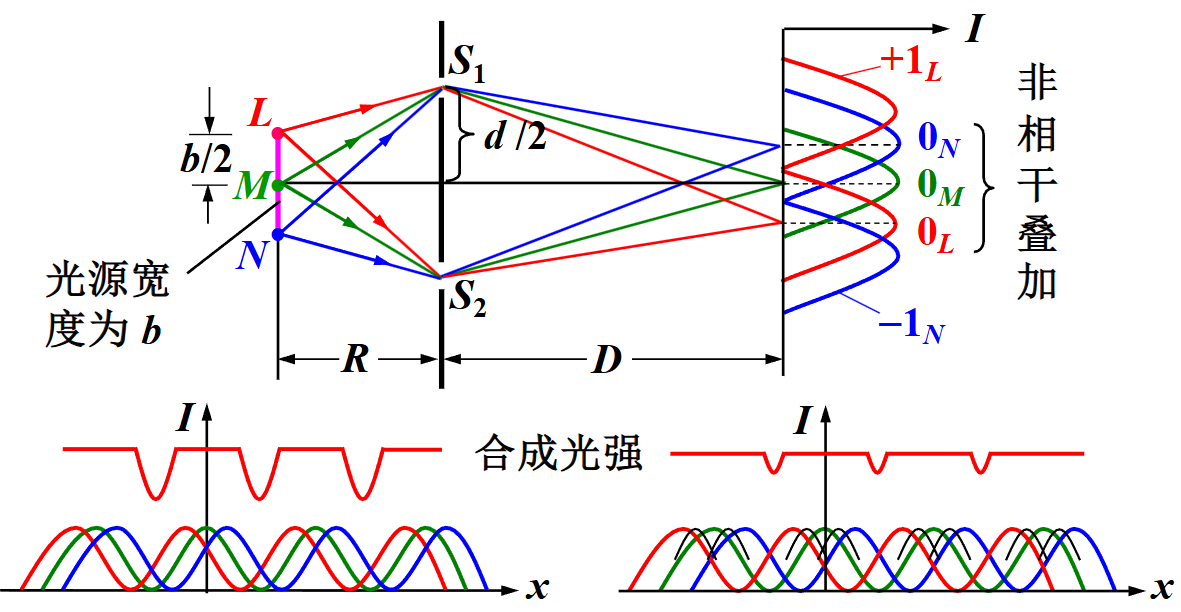
如上图所示,固定双缝宽度 d,考虑光源宽度,那光源并不完全位于双缝的中轴线上,也即波程差需要考虑在到达双缝前后两个阶段,即:
δ=left(r2′−r1′)+right(r2−r1)
在右侧板的同一个位置,r2−r1=0,基于此有如下事实:
光源各点的波在右侧同一点的相位差,最大值为 L,N 两点的相位差,因此当这两点的相位差超过 2π 的时候,这一点的相位集合会囊括 [0,2π],因此合成光强变为常数,干涉条纹消失
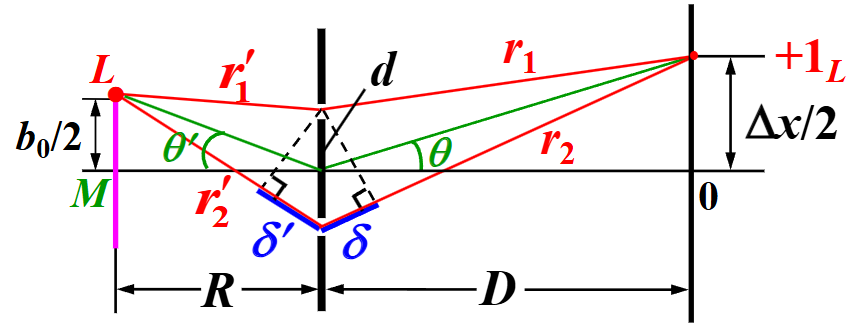
因此,当干涉条纹恰好消失的时候,应满足:
N0N−1N0+L0L1−L0=L1=L0=0=Δx
解出 L1=2Δx=2dDλ
如上图,根据 D>>d 及 R>>d,b0 有:
r2−r1r2′−r1′≈dsinθ≈dtanθ=d⋅2DΔx=2λ≈dsinθ′≈dtanθ=d⋅2Rb0
这样代入 δ 的表达式,并且根据 1 级明纹处 δ=λ 有:
b0=dRλ
这被称为光源极限宽度
相干间隔和相干孔径角
根据上面的思路,固定光源宽度 b,同理可以得到双缝间距的要求:
d0=bRλ
这被称为相干间隔,物理意义是:光场中正对光源的平面上,能够产生干涉的两个次波源间的最大距离
这个过程也能用相干孔径角来代替,即光源中心点到两个缝的夹角:
θ0≈2tan2θ0=Rd0=bλ
光程
由于光在不同介质中,波长会被改变,因此当波程差相同的时候,不同介质中的相位差会有所不同
为了保证一致性,我们定义光程为:在折射率为 n 的介质中,光走距离 r 的等效真空路程,公式为
L=nr
这样相位差公式可以写成:
Δφ=ΔL⋅λ2π
其中 λ 为真空中波长
薄膜干涉
薄膜干涉指的是光波在照射到透明薄膜(如水面上的油膜、肥皂泡)时,经薄膜上、下表面反射后相互叠加,从而形成光强重新分布的现象
由于一般化的薄膜干涉非常复杂,在此只讨论:
- 厚度不均匀薄膜产生的在表面处的等厚条纹
- 厚度均匀薄膜产生的在无穷远处的等倾条纹
等厚条纹
假设薄膜内的折射率为 n,外部为 n′,当光线以 i 的入射角进入时,折射角为 r
在薄膜上任取一点 P,假设厚度为 e,则在该点应该有一束直接反射光和一束间接反射光,如下图:
有光程差:
δ≈2necosr+2λ=2en2−n′2sin2i+2λ
最后的 λ/2 是因为半波损失
实际中常采用单色平行光正入射照明方式,即认为 i=r=0,简化为:
δ≈2ne+2λ
劈尖
指由夹角 θ 很小的两个平面构成的薄膜,可近似认为膜上一点 P 到边缘的距离和该点厚度满足:
Le≈sinθ≈θ
和之前类似,δk=kλ 的时候为亮纹,因此,相邻两个亮纹之间的厚度差和条纹间距为:
Δe=2nλ⟹L=θΔe=2nθλ
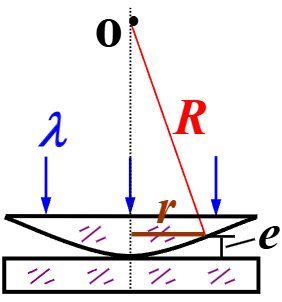
牛顿环
如上图所示,平凸透镜与平晶形成空气劈尖,可以看出:
r2=R2−(R−e)2≈2Re⟹e≈2Rr2
由于劈尖成环状,因此形成了明暗相间的环,半径为:
明环rk=2(2k−1)Rλk∈N+暗环rk=kRλk∈N
一般在实际测量中用作差的方式规避知道确切级次:
rk+m2−rk2=mRλ
等倾干涉
考虑薄膜厚度固定为 e 的情况,此时两束反射光平行,需要利用一个透镜在焦平面上观察干涉条纹
此时也可得到:
δ≈2necosr+2λ=2en2−n′2sin2i+2λ
因此 δ 只跟 i 有关,因此被称为等倾条纹,其性质为:
- 形成的是明暗相间同心圆环,半径 Rk=ftanik,其中 f 为焦距
- 环半径越小,级次越高,并且距离是内疏外密
- 膜厚增大时,条纹要向外扩展,且中心亮纹级次变化为 1 时,膜厚变化:
Δe=2nλ
利用等倾干涉,可以实现增透膜或增反膜,例如:
- 在相机的镜头表面镀膜,使得光线进入时,在膜上下表面的反射光发生相消干涉,以增强透射光
- 在墨镜的表面镀膜,让透射光相消干涉,增强反射光
折射率为 ne 的增透膜的厚度应该满足:
2nee=(2k+1)2λ⟹e=(2k+1)4neλ,k∈N
而如果考虑振幅,则可以证明反射光完全消除的时候,介质折射率应满足 ne=nn0
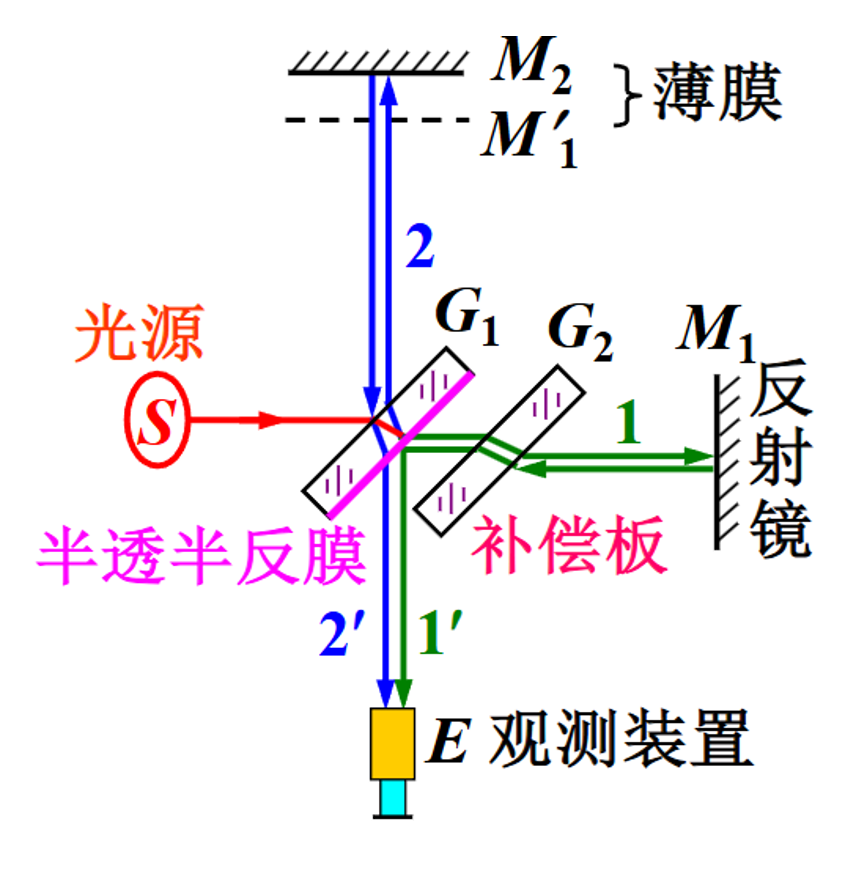
迈克尔孙干涉仪
如上图,M1′ 和 M2 构成薄膜的两个面,其平行时为等倾条纹,有小夹角时为等厚条纹
可以通过干涉条纹的数目变化 N 测量出系统发生的变化:
- 平面镜 M1 发生平移 Δd:
Δd=N⋅2λ
- 光路 1 中插入了折射率为 n 的介质:
2(n−1)l=Nλ