大学物理 光的衍射

Chapter B - 光的衍射

惠更斯 - 菲涅尔原理

光的衍射

光在传播过程中能绕过障碍物的边缘，进入几何阴影区继续传播，且光强在空间重新分布的现象叫光的衍射

衍射是波的一种特性，能否观察到明显的衍射，取决于障碍物或开口的尺寸与波长的对比关系，当障碍物的尺寸和光的波长相近的时候，所形成的图案并不遵循“光走直线”，而是产生了明暗相间的图案，这被称为衍射图案

记光源 $S$ 到障碍物 $B$ 的距离为 $L$ ，障碍物到观察屏 $P$ 的距离为 $D$ ，则衍射可以分类为：

菲涅尔衍射（近场衍射）： $L, D$ 至少有一个是有限值
夫琅禾费衍射（远场衍射）： $L, D$ 都是无限值，这需要通过透镜来实现

惠更斯原理

波面上的点作为子波源：在波传播过程中的任一时刻，波阵面上的每一个点都可以被视为一个新的点波源，这些点波源会向四面八方发射球面波（称为子波）
包络面形成新波面：这些子波在传播了一小段时间后，它们的外包络面就构成了下一个时刻的新的波阵面
波面间距：相邻两个波阵面之间的空间距离等于波的传播速度 $v$ 乘以波传播所经历的时间间隔 $\Delta t$

其中，波面是指那些等相位点形成的面，与光的传播方向垂直，又被称为波前

惠更斯原理无法定量解释干涉和衍射

菲涅尔修正

波传到的任何一点都是子波的波源，各子波在空间某点的相干叠加，决定了该点的波强

在波前上的任意一点 $Q$ 处选择任意面元 $\mathrm{d}S$ ，则其对空间任意一点 $P$ 的振动贡献为：

\mathrm{d}E(P) = \underline{\frac{a(Q)\cdot K(\theta)}{r}\cdot\mathrm{d}S}\cdot \cos\left(\omega t - \frac{2\pi r}{\lambda}\right)

横线项为振幅贡献，后面的是相位贡献

其中：

$a(Q)$ 表示 $Q$ 处的子波源强度，取决于原始波在 $Q$ 的振幅
$r$ 是 $P, Q$ 距离， $\theta$ 表示 $\mathrm{d}S$ 法方向 $\vec{n}$ 与 QP 径矢 $\vec{r}$ 的夹角
$K(\theta)$ 为方向因子，在 $\theta = 0$ 时最大，单调递减，当 $\theta \geq \dfrac{\pi}{2}$ 时 $K(\theta) = 0$

在 $P$ 点，合振动可以对波面求积分得到，形式可以表示为：

E(P) = E_0(P)\cos\big(\omega(t) + \varphi(P)\big)

具体的数学推导由基尔霍夫完成，被称为菲涅尔-基尔霍夫公式

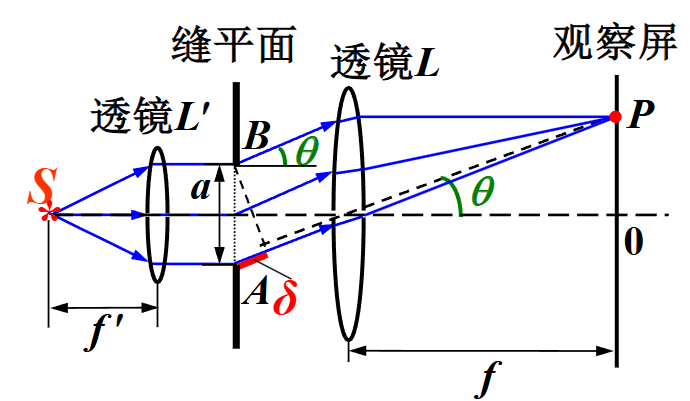
单缝夫琅禾费衍射

观察夫琅禾费衍射的装置图

下面给出两种确定条纹的方法：

半波带法

可以近似认为， $A$ 和 $B$ 处的光程差为：

\delta = a\sin\theta

由于两列光的光程差为 $\lambda / 2$ 时，其相位差为 $\pi$ ，恰好发生相消干涉

因此，假设：

\delta = a\sin\theta = k\cdot \frac{\lambda}{2},\quad k \in \mathbb{N}

当 $k > 0$ 的时候，我们可以将缝等分成 $k$ 份，每一份称为一个半波带，相邻的两个半波带光程差恰好为波长的一半 $\lambda / 2$ ，发生相消干涉

因此：

$k$ 为奇数的时候，两两分组之后还会有一个半波带剩余，每一组的两条半波带相消，最后一个半波带的光形成明纹
$k$ 为偶数的时候，两两分组之后不会有半波带剩余，每一组的两条半波带相消，形成了暗纹
$k = 0$ 的时候，对应 $\theta = 0$ ，也即对应中心明纹

半波带法给出的中央明纹（中心）和暗纹位置是准确的，其余明纹中心的位置稍有偏差

光强求极值法

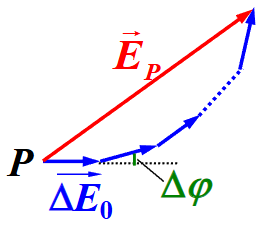
首先求光强，将缝等分成 $N$ 份， $N$ 充分大，可以认为各个窄带的子波在 $P$ 的振幅近似相等，记为 $\Delta E_0$

相邻子波的相位差为：

\Delta\varphi = \frac{2\pi}{\lambda}\cdot\Delta x\sin \theta = \frac{2\pi}{\lambda}\cdot\frac{a}{N}\sin\theta

由于 $N$ 充分大，可以认为 $\Delta\varphi < 2\pi$

因此 $P$ 点实际上是多个简谐振动的合成，不同振动之间仅有初相位不同，合成图像为：

振幅的合成

当 $\theta = 0$ 即 $\Delta\varphi = 0$ 的时候，这些振幅矢量都共线，因此合成后 $E_0 = N\Delta E_0$

对于其他点，当 $N\to\infty$ 的时候， $\Delta\varphi \to 0$ ，因此这个折线段会变成圆弧，圆心角实际上就是所有的 $\Delta\varphi$ 求和，即：

\Delta\varPhi = N\Delta\varphi = \frac{2\pi a}{\lambda}\sin\theta

因此：

E_p = 2R\sin\frac{\Delta\varPhi}{2}

而这个圆弧的总长度是所有振幅矢量的模求和，即：

R\Delta\varPhi = N\Delta E_0 = E_0

解出最终结果：

E_p = \frac{2E_0}{\Delta\varPhi}\sin\frac{\Delta\varPhi}{2}

令：

\alpha = \frac{\Delta\varPhi}{2} = \frac{\pi a\sin\theta}{\lambda}

则：

E_p = E_0\cdot\frac{\sin\alpha}{\alpha}

其中 $E_0$ 为中心点振幅

因此，设中心点强度为 $I_0$ ，则有：

I = \begin{cases} I_0 & \alpha = 0 \\[1em] I_0 \cdot\left(\dfrac{\sin\alpha}{\alpha}\right)^2 & \alpha > 0\end{cases}

因此，明纹对应 $I$ 的极大值点，暗纹对应 $I$ 的零点，这也解释了为什么半波带法求出的明纹位置只有中心明纹是准确的： $\sin\alpha$ 取到 1 无法保证 $I$ 取到极大值，求导可以得到，极大值点应满足：

\tan\alpha = \alpha

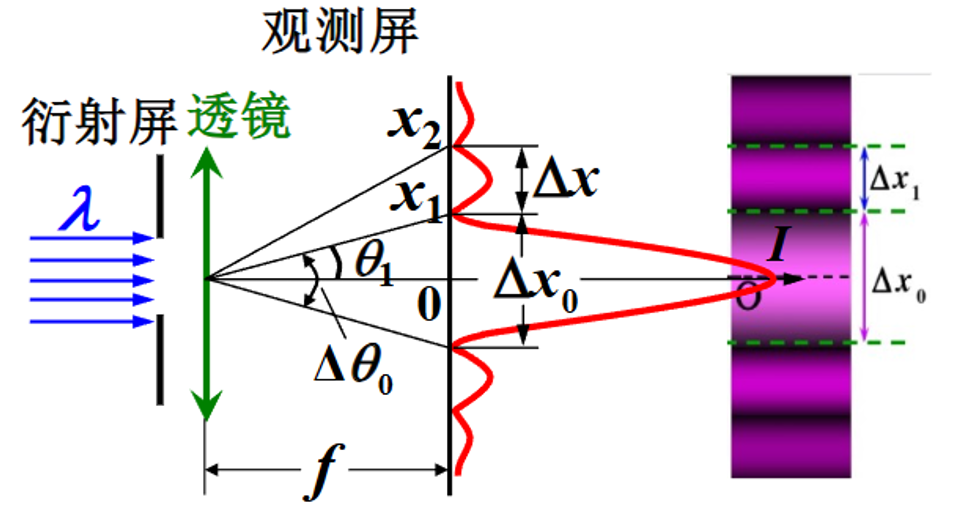
纹路宽度

中心明纹角宽度与线宽度示意图

对于中心明纹，其宽度等于级次绝对值最低的两条暗纹之间的距离，这两条暗纹满足：

a\sin\theta_1 = \lambda

对于 $\theta_1$ 很小的情况，有 $\sin\theta_1 \approx \tan\theta_1 \approx \theta_1$

因此角宽度和线宽度分别为：

\begin{align*}\Delta\theta_0 &= 2\theta_1 \approx 2\sin\theta_1 = \frac{2\lambda}{a} \implies \boxed{a\Delta\theta_0 = 2\lambda} \\\Delta x_0 &= 2f\tan\theta_1 \approx 2f\sin\theta_1 = \frac{2f\lambda}{a}\implies \boxed{a\Delta x_0 = 2f\lambda}\end{align*}

其中后两个式子被称为衍射反比率

当衍射角 $\theta$ 很小的时候，暗纹中心位置为：

x_k = f\tan\theta_k \approx f\sin\theta_k = \frac{kf\lambda}{a}

因此明纹宽度：

\Delta x \approx \frac{f\lambda}{a} = \frac{1}{2}\Delta x_0

直观上来看，中心明纹是由对称的两个明纹拼接而成，中间没有暗纹，自然宽度就是次级明纹的两倍

光栅衍射

光栅是由大量的等宽等间距的平行狭缝（或反射面）构成的光学元件，并且可以推广，由衍射单元排列成的具有空间周期性的任何结构都可叫作光栅

按照元件本身是透光的还是反光的，可以将其分成透光光栅和反光光栅

光栅的空间周期被称为光栅常数 $d = a + b$ ，其中：

$a$ 为透光（或反光）部分的宽度，例如平行狭缝的宽度
$b$ 为不透光（或不反光）部分的宽度，例如平行狭缝的间距

光栅夫琅禾费衍射

主极大和暗纹位置

忽略每个缝独立的衍射，考虑这些缝之间发生的多光束干涉

假设光栅一共有 $N$ 个缝，则相邻缝衍射光的光程差为：

\delta = d\sin\theta

当相邻缝的光程差为 $\pm k\lambda$ 即相位差为 $\pm 2k\pi$ 的时候，每个缝的衍射光都产生了相长干涉，在这些位置能产生非常显著的明纹，被称为主极大，条件为：

d\sin\theta = \pm k\lambda,\quad k \in \mathbb{N}

同样的，也可以利用上述光强求极值法中的矢量合成思想来考虑，近似每个缝的衍射光到达 $P$ 点的振幅都是 $E_p$ ，相邻缝的相位差为：

\Delta\varphi = 2\pi\cdot\frac{d\sin\theta}{\lambda}

那主极大的条件实际上是所有矢量共线，也即 $\Delta\varphi = \pm2k\pi$ ，与之前的结果相同

那根据这个思路，以及近似认为每个缝的衍射光振幅相同，我们可以得到形成暗纹的条件为，这些振幅矢量构成了闭合正多边形，即：

N\Delta\varphi = \pm2k'\pi,\quad k'\in\mathbb{N},\,\,k\nmid N

可以解出来暗纹方程：

\begin{align*}d\sin\theta = \pm\frac{k'}{N}\lambda,\quad &k'\in\mathbb{N},\,\,k\nmid N \\[1em]\implies d\sin\theta = \pm k\lambda + \frac{m}{N}\lambda,\quad &k\in\mathbb{N},\,\,m = 1, 2, \dots, N - 1\end{align*}

主极大半角宽

主极大半角宽等于主极大对应的衍射角与相邻第一暗纹对应的衍射角之差 $\Delta\theta$

首先根据主极大方程和暗纹方程， $k$ 级主极大和其相邻暗纹满足：

\begin{align*} d\sin\theta_k &= k\lambda \\ d\sin(\theta_k + \Delta\theta) &= k\lambda + \frac{\lambda}{N} \end{align*}

相减之后，根据微分的定义可以近似得到：

d\cos\theta_k\Delta\theta \approx \frac{\lambda}{N} \implies \Delta\theta = \frac{\lambda}{Nd\cos\theta_k}

单缝调制

在上述的分析过程中，我们没有考虑光栅每个缝各自的影响，而实际情况下，干涉条纹的各级主极大的强度将不再相等，而是受到衍射的调制

例如在单缝衍射的暗纹处，衍射光的光强为 0，也即无论干涉情况如何，这里都会是暗纹，如果此处恰好和主极大的位置重叠，那这个主极大将会消失，称之为缺级

分别写出 $k$ 级主极大方程与 $k'$ 级衍射暗纹方程

\begin{align*} d\sin\theta &= k\lambda \\ a\sin\theta' &= k'\lambda \end{align*}

如果这两个位置重叠，即 $\theta = \theta'$ ，则：

\frac{d}{a} = \frac{k}{k'} \implies k = \frac{d}{a}k',\quad k'\in \mathbb{N}

这里的 $k$ 也就是会消失的主极大级数

光强

根据之前的讨论可以得到，每个缝在某点的光强为：

E_{Pi} = E_{0i}\cdot\frac{\sin\alpha}{\alpha},\quad \alpha = \frac{\pi a\sin\theta}{\lambda}

而相邻缝的相位差是：

\Delta\varphi = 2\pi\cdot\frac{d\sin\theta}{\lambda}

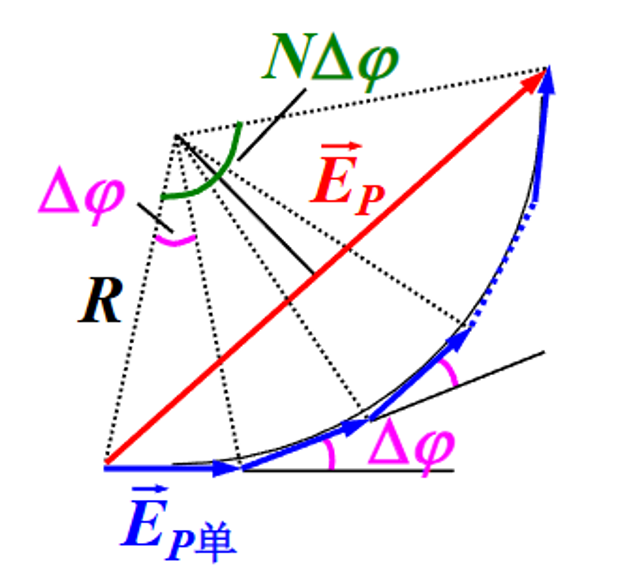
同样利用矢量合成的思路，可以对这 $N$ 个缝的光强进行合成，注意此处不能认为 $N$ 充分大

光栅夫琅禾费衍射的光强合成

如上图，有：

\begin{align*} E_{Pi} &= 2R\sin\frac{\Delta\varphi}{2} \\[1em] E_P &= 2R\sin\frac{N\Delta\varphi}{2} \end{align*}

令 $\beta = \Delta\varphi / 2$ ，可以得到合光强为：

E_p = E_{Pi}\cdot\frac{\sin N\beta}{\sin\beta} = E_{0i}\cdot\frac{\sin\alpha}{\alpha}\cdot\frac{\sin N\beta}{\sin\beta}

设 $I_{0i}$ 是单缝衍射中央明纹中心光强，则光栅夫琅禾费衍射任意一点光强为：

I_P = I_{0i}\cdot\left(\frac{\sin\alpha}{\alpha}\right)^2\cdot\left(\frac{\sin N\beta}{\sin\beta}\right)^2

其中：

\alpha = \frac{\pi a\sin\theta}{\lambda},\quad \beta = \frac{\pi d\sin\theta}{\lambda}

我们将 $\left(\dfrac{\sin\alpha}{\alpha}\right)^2$ 称为单缝衍射因子， $\left(\dfrac{\sin N\beta}{\sin\beta}\right)^2$ 称为多光束干涉因子

斜入射光栅方程

考虑斜入射到达光栅，入射角为 $i$ ，则很容易得知相邻缝的光程差变为：

\delta = d(\sin\theta - \sin i)

相应的，主极大方程变为：

d(\sin\theta - \sin i) = \pm k\lambda

按照如下方式规定 $i, \theta$ 的方向：

光栅指向透镜和观察屏的一侧为法向正方向，设法向方向为 $\hat{\mathbf{n}}$
当 $i, \theta$ 绝对值减小的时候，如果对应光线是顺时针转向 $\hat{\mathbf{n}}$ 则为正，反之为负
可以记为叉乘结果垂直纸面向外的为负

光学仪器的分辨本领

圆孔的夫琅禾费衍射

对于一般的光学仪器，光线通过直径为 $D$ 的孔入射，而这个小孔会在观察屏上产生衍射，衍射图像是中央亮斑加上明暗交替的环，中央亮斑被称为艾里斑

根据菲涅尔-基尔霍夫公式，可以得到 1 级暗环的衍射角满足：

D\sin\theta \approx 1.22\lambda

$\theta_1$ 也被称为艾里斑半角宽

透镜的分辨本领

考虑衍射和干涉现象时，物体的每一个点会对应象上的一个斑，因此透镜的分辨能力会被限制，具体由瑞利判据给出：

对两个等光强的非相干物点，如果它们的一个象斑中心恰与另一个象斑边缘（第一暗纹处）重合，则两物点刚可分辨，象斑再近则两物点不能分辨

因此对于一个透镜来说，其能够分辨的物点最小夹角恰好是艾里斑半角宽（考虑两个物点经过透镜中心的光），即最小分辨角：

\theta_{\min} = \theta_1 \approx 1.22\frac{\lambda}{D}

定义透镜的分辨本领为最小分辨角的倒数：

R \equiv \frac{1}{\theta_{\min}} \approx \frac{D}{1.22\lambda}

因此大型望远镜可以通过提升 $D$ 来提升分辨本领，而显微镜则需要通过降低 $\lambda$ 来提升，例如使用电子，其德布罗意波长远小于可见光波长

光栅的分辨本领

角色散本领

由于光栅的主极大条件为：

d\sin\theta_k = k\lambda

因此对于不同颜色的可见光，其主极大的位置不同，因此光栅可以产生色散，按照如下方式定义角色散本领：

对于波长为 $\lambda$ 和 $\lambda + \Delta\lambda$ 的两束光，其 $k$ 级谱线的衍射角分别为 $\theta$ 和 $\theta + \Delta\theta$ ，则角色散本领为：

D_\theta \equiv \frac{\Delta\theta}{\Delta\lambda}

对光栅的主极大条件两边求微分，可以得到光栅的角色散本领：

D_\theta = \frac{k}{d\cos\theta_k}

角色散本领的物理意义是，其值越大，不同波长的光分开的角度越大

色分辨本领

假设光栅能分辨的最小波长差为 $\Delta\lambda$ ，则定义其色分辨本领为：

R\equiv\frac{\lambda}{\Delta\lambda}

根据瑞利判据，这两个波长的光此时应该恰好满足：其同级主极大的衍射角之差等于主极大半角宽，即：

\Delta\theta = \frac{\lambda}{Nd\cos\theta_k}

因此：

R = \frac{\lambda}{\Delta\lambda} = \frac{\lambda D_\theta}{\Delta\theta} = Nk

X 射线衍射

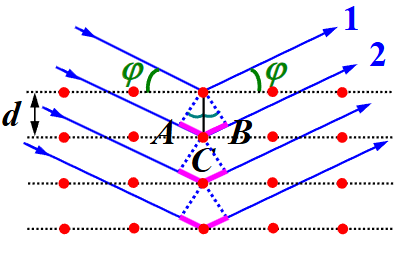
由于 X 射线的波长极短，因此只有用晶体产生衍射，而在考虑晶体衍射的时候，需要考虑同层晶面内衍射光的干涉和相互平行的晶面间衍射光的干涉

首先可以证明，在同层晶面内，0 级主极大的方向，就是以这层晶面为镜面的反射线方向，也即符合反射定律

之后考虑相互平行的晶面间，0 级主极大衍射光（即反射光）之间的干涉

相互平行的晶面间多束反射光的干涉

如上图，假设晶面间距是 $d$ ，掠射角为 $\varphi$ ，则光程差为：

\delta = \overline{AC} + \overline{CB} = 2d\sin\varphi

因此主极大条件为：

2d\sin\varphi = k\lambda

这被称为布拉格公式

可以证明，所有晶面族的布拉格条件，完备地表达了晶体 X 射线衍射的主极大分布情况，也即不需要考虑相互平行的晶面间其他级次主极大的干涉

本文采用署名-非商业性使用-相同方式共享 4.0 国际许可协议，转载请注明出处。