大学物理 原子中的电子

Chapter F - 原子中的电子

氢原子的量子力学处理

氢原子可见光光谱如下：

氢原子可见光光谱

其中 $1 \mathrm{\AA} = 0.1\rm nm$

对于可见光区的光谱线，可以用巴尔末经验公式来描述：

$$\tilde{\nu} = \frac{1}{\lambda} = \frac{4}{B}\left(\frac{1}{2^2} - \frac{1}{n^2}\right) ,\quad B = 3645.6\rm\AA$$

其中 $\tilde{\nu}$ 被称为波数

其可以扩展到非可见光区，得到里德伯方程：

$$\tilde{\nu} = R\left(\frac{1}{n^2} - \frac{1}{n'^2}\right) ,\quad R = \frac{4}{B},\,\, n', n \in \mathrm{N}^{+},\,\,n' > n$$

$n = 2$ 对应巴尔末方程，这个谱线系被称为巴耳末系

玻尔的氢原子理论

玻尔量子化了轨道的角动量，即：

$$L_n = mv_nr_n = n\hbar$$

结合库仑力提供向心力公式：

$$\frac{e^2}{4\pi\varepsilon_0r_n^2} = m\frac{v_n^2}{r_n}$$

可以得到轨道半径和能量的关系：

$$\begin{align*} r_n = n^2 r_1 &= n^2\frac{4\pi\varepsilon_0\hbar^2}{me^2} \\ E_n = \frac{1}{n^2}E_1 &= \frac{1}{n^2}\cdot\frac{-me^4}{2(4 \pi\varepsilon_0)^2\hbar^2} \end{align*}$$

氢原子释放光子即为不同能级之间的跃迁，频率为：

$$\nu = \frac{E_i - E_j}{h} = \frac{E_1}{h}\left(\frac{1}{n_i^2} - \frac{1}{n_j^2}\right)$$

与里德伯公式是符合的，常数也与实验值一致

但是玻尔理论只能解释氢原子或者类氢离子，不具有拓展性

量子力学处理

解定态薛定谔方程，首先，电子在原子核的电场中，势能为：

$$U(r) = -\frac{e^2}{4\pi\varepsilon_0 r}$$

球坐标系下的 $\nabla^2$ 算子表达式为：

$$\nabla^2 = \frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial}{\partial r} \right) + \frac{1}{r^2 \sin\theta} \frac{\partial}{\partial \theta} \left( \sin\theta \frac{\partial}{\partial \theta} \right) + \frac{1}{r^2 \sin^2\theta} \frac{\partial^2}{\partial \varphi^2}$$

为了简化这一坨，我们定义：

$$\hat{L}^2 = -\hbar^2 \left[ \frac{1}{\sin\theta} \frac{\partial}{\partial\theta} \left( \sin\theta \frac{\partial}{\partial\theta} \right) + \frac{1}{\sin^2\theta} \frac{\partial^2}{\partial\varphi^2} \right]$$

再定义：

$$\hat{L}_z = -\hbar \frac{\partial}{\partial\varphi}$$

则得到：

$$\hat{L}^2 = -\frac{\hbar^2}{\sin\theta} \frac{\partial}{\partial\theta} \left( \sin\theta \frac{\partial}{\partial\theta} \right) + \frac{\hat{L}_z^2}{\sin^2\theta}$$

代入原来的表达式得到：

$$\nabla^2 = \frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial}{\partial r} \right) - \frac{\hat{L}^2}{r^2 \hbar^2}$$

因此能量本征方程为：

$$\hat{H} \Psi = \left\{ -\frac{\hbar^2}{2m} \left[ \frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial}{\partial r} \right) - \frac{\hat{L}^2}{r^2 \hbar^2} \right] - \frac{e^2}{4\pi\varepsilon_0 r} \right\}\Psi= E\Psi$$

由于 $\hat{L}$ 与 $r$ 无关，因此可以使用分离变量法求解，令：

$$\Psi(r, \theta, \varphi) = R(r)Y_{l, m_l}(\theta, \varphi)$$

代入能量本征方程后，得到：

$$\frac{1}{R} \frac{\mathrm{d}}{\mathrm{d}r} \left( r^2 \frac{\mathrm{d}R}{\mathrm{d}r} \right) + \frac{2m r^2}{\hbar^2} \left( E + \frac{e^2}{4\pi\varepsilon_0 r} \right) = \frac{1}{Y} \left(\frac{\hat{L}^2}{\hbar^2}Y\right)$$

方程左边只依赖于 $r$，右边只依赖于 $\theta$ 和 $\phi$。要使这个等式对所有 $r, \theta, \phi$ 都成立，两边必须等于同一个常数 $\lambda$

角动量量子化

对原式右边进行化简可以得到：

$$\hat{L}^2Y = \lambda\hbar^2Y = L^2Y, \quad L \in \mathbb{R}$$

这实际上就是 $\hat{L}^2$ 的能量本征方程

通过高级数学技巧可以得到 $\hat{L}^2$ 本征值为 $l(l + 1)\hbar^2$，$\hat{L}_z$ 的本征值为 $m_l\hbar$，二者的本征函数均为球谐函数，也就是这里的 $Y$

这也告诉了我们 $\lambda = l(l + 1)$，能够帮助解出径向方程

我们将 $l$ 称为角量子数，其描述的实际上是粒子角动量的大小，值为：

$$L = \sqrt{l(l + 1)}\hbar$$

而 $m_l$ 被称为磁量子数，其描述的是角动量的空间取向，取值为：

$$m_l = 0, \pm 1, \cdots \pm l$$

每种本征值对应一条 z 轴，这说明角动量共有 $2l + 1$ 种取向

而原式中的 $Y_{l, m_l}(\theta, \varphi)$ 被称为 $\hat{L}^2$ 和 $\hat{L}_z^2$ 的共同本征函数，可以解出其为球谐函数，而球谐函数的表达式为：

$$Y_l^m(\theta, \phi) = C_{l, m_l} P_l^m(\cos\theta) e^{i m \phi} = \sqrt{\frac{(2l+1)}{4\pi} \frac{(l-m)!}{(l+m)!}} P_l^m(\cos\theta) e^{i m \phi}$$

其中 $C_{l, m_l}$ 是归一化系数，$P_l^{m_l}$ 是关联勒让德多项式

球谐函数前几种可能的取值为：

$$\begin{align*} Y_{0, 0} &= \frac{1}{\sqrt{4\pi}} \\[1em] Y_{1, 0} &= \sqrt{\frac{3}{4\pi}} \cos\theta\\[1em] Y_{1, \pm 1} &= \mp \sqrt{\frac{3}{8\pi}} \sin\theta e^{\pm i\phi} \end{align*}$$

实际上，他们分别对应的是 $1s$ 轨道、$2p_z$ 轨道与 $2p_x, 2p_y$ 轨道

主量子数

代入 $\lambda = l(l + 1)$，对左边经过魔术技巧可以得到：

$$\left[\frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}+\frac{2m}{\hbar^{2}}\left(E+\frac{e^{2}}{4\pi\varepsilon_{0}r}\right)-\frac{l(l+1)}{r^{2}}\right][r\cdot R(r)]=0$$

其中 $l$ 为角量子数

可以解得能量本征值为

$$\begin{align*} E_n = \frac{1}{n^2}E_1 &= \frac{1}{n^2}\cdot\frac{-me^4}{2(4 \pi\varepsilon_0)^2\hbar^2} \approx \frac{-13.6\,\,\mathrm{eV}}{n^2} \end{align*}$$

可以看出与玻尔得到的表达式是相同的，在这之中，我们把 $n\in\mathbb{N}^{+}$ 称之为主量子数，其决定了粒子的能量

有了主量子数之后，角量子数需要满足：

$$l = 0, 1, \cdots, n - 1$$

概率分布

通过以上的分析可以得出，电子的波函数为：

$$\Psi_{n,l,m_l}(r, \theta, \varphi) = R_{n,l}(r)\cdot Y_{l, m_l}(\theta, \varphi)$$

由归一化条件可以得到：

$$\int_{\text{全空间}} \left| \psi_{nlm_l}(r,\theta,\varphi) \right|^2 \cdot r^2 \, \mathrm{d}r \sin\theta \, \mathrm{d}\theta \, \mathrm{d}\varphi = 1$$

分离变量，并利用立体角元 $\mathrm{d}\Omega = \sin\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi$ 可以得到：

$$\int_0^\infty \left| R_{nl}(r) \right|^2 r^2 \, \mathrm{d}r \cdot \int_0^{4\pi} \left| Y_{lm_l}(\theta,\varphi) \right|^2 \, \mathrm{d}\Omega = 1$$

这实际上是要求在径向上和角向上都满足归一化条件，于是可以分别得到：

• 径向概率分布：表示电子出现在 $r\sim r + \mathrm{d}r$ 之间的概率，表达式为：

$$\left| R_{nl}(r) \right|^2 r^2 \, \mathrm{d}r \cdot \int_0^{4\pi} \left| Y_{lm_l}(\theta,\varphi) \right|^2 \, \mathrm{d}\Omega = \left| R_{nl}(r) \right|^2 r^2 \, \mathrm{d}r$$

• 角向概率分布：表示电子出现在 $(\theta, \varphi)$ 方向的立体角 $\mathrm{d}\Omega$ 范围内的概率，表达式为：

$$\int_0^\infty \left| R_{nl}(r) \right|^2 r^2 \, \mathrm{d}r \cdot \left| Y_{lm_l}(\theta,\varphi) \right|^2 \, \mathrm{d}\Omega = \left| Y_{lm_l}(\theta,\varphi) \right|^2 \, \mathrm{d}\Omega$$

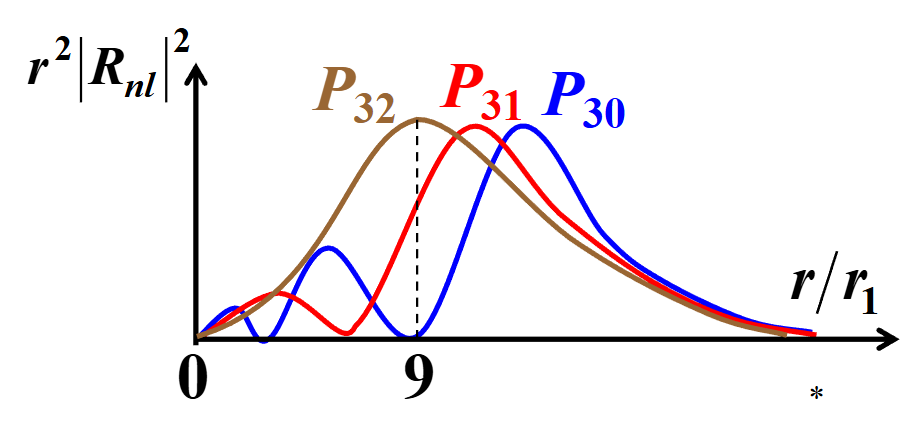
对于固定了 $(n, l)$ 的径向分布，可以求导得出其概率分布的最大值，经过计算可以发现，对于 $l = n - 1$ 的状态，其极大值点恰好满足玻尔理论，也即例子出现概率最大的位置是：

$$r_n = n^2 r_1 = n^2\frac{4\pi\varepsilon_0\hbar^2}{me^2}$$

并且对于固定了 $(n, l)$ 的径向分布图像，一共会有 $n - l$ 个峰值，例如：

径向分布概率图

电子自旋

斯特恩 — 盖拉赫实验

目的是证明角动量的空间量子化，首先利用磁矩与角动量的关系：

$$\vec{\mu} = I\overrightarrow{S} = -I\pi r^2\vec{e}_L = -\frac{e}{2m}\overrightarrow{L}$$

其中利用了旋转电子的电流公式：

$$I = \frac{\mathrm{d}q}{\mathrm{d}t} = \frac{e}{(2\pi r) / v} = \frac{ev}{2\pi r}$$

因此有：

$$\mu_z = -\frac{e}{2m_e}L_z = -\frac{e\hbar}{2m_e}m_l = -\mu_B m_l$$

其中 $\mu_B$ 为玻尔磁子，定义为：

$$\mu_B = \frac{e\hbar}{2m_e}$$

这表明磁矩的取向也是固定的 $2l + 1$ 种，因此在一维变化的外磁场中，磁矩的受力方向也是量子化的：

$$F_z = -\frac{\partial W}{\partial z} = -\frac{\partial(-\vec{\mu}\cdot\overrightarrow{B})}{\partial z} = \mu_Bm_l\frac{\partial B}{\partial z}$$

因此可以通过测量原子束在变化磁场中的受力证明角动量量子化

但在一些实验中，$l = 0$ 的态分裂出了两条线，这与 $2l + 1 = 1$ 是矛盾的，因此提出了电子自旋理论

电子自旋

电子不是质点，而是有固有的自旋角动量 $\overrightarrow{S}$ 和自旋磁矩 $\vec{\mu}$，其自旋不是小球自转，在经典力学中没有对应的理论，而是电子的“内禀”运动，其对应着自旋量子数 $s$ 与自旋磁量子数 $m_s$，计算方式和轨道角动量是类似的

根据斯特恩 — 盖拉赫实验，电子的 $m_s$ 有两种取值，因此 $2s + 1 = 2$，得到电子的自旋量子数为 $s = 1 / 2$，因此：

$$S = \sqrt{s(s + 1)}\hbar = \frac{\sqrt{3}}{2}\hbar,\quad S_z = m_s\hbar = \pm \frac{1}{2}\hbar$$

而高深的量子力学可以推导出电子的自旋磁矩：

$$\vec{\mu}_s = -\frac{e}{m_e}\overrightarrow{S} \implies \mu_{sz} = -\frac{e}{m_e}S_z = \mp \frac{e\hbar}{2m_e} = \mp \mu_B$$

自旋 - 轨道耦合

即总角动量是由自旋角动量和轨道角动量耦合而成：

$$\overrightarrow{J} = \overrightarrow{L} + \overrightarrow{S}$$

此处的加号并不是经典的矢量求和

根据量子力学，$\overrightarrow{J}$ 也是量子化的，并且形式上和 $\overrightarrow{L}, \overrightarrow{S}$ 都相同，令 $j$ 是总角动量量子数，则 $j, l, s$ 的关系是：

$$j = \begin{cases} s = \dfrac{1}{2} & l = 0 \\[1em] l + s = l + \dfrac{1}{2} & \overrightarrow{L}, \overrightarrow{S} \text{ 同向}\\[1em] l - s = l - \dfrac{1}{2} & \overrightarrow{L}, \overrightarrow{S} \text{ 反向} \end{cases}$$

原子状态表示法

形如：

$$n\,\,{}^{2s + 1}\boxed{}_j$$

其中，方框中填写的轨道量子数对应的轨道代号，例如 $s,p,d,f$ 等

举个例子，对于 $n = 3, l = 1, s = 1 / 2, j = 3 / 2$ 的原子，其状态为：

$$3\,\,{}^{2}\mathrm{p}_{3/2}$$

碱金属原子光谱

对于碱金属来说，非价电子与原子核一起形成了一个带 $+e$ 的结构，被称为原子实，这种结构与氢原子是类似的

• 轨道贯穿：价电子有概率进入原子实内部，感受到更强的有效核电荷，平均势能降低，能级下移。对低 $l$ 态，特别是 $s$ 态的影响显著
• 原子实极化：价电子在外部极化原子实，产生诱导偶极矩，额外的吸引势能使平均势能降低，能级下移

由于轨道贯穿与原子实极化两种现象的存在，碱金属的能级与 $n, l$ 都有关系，其能级公式为：

$$E_nl = \frac{-13.6\,\,\mathrm{eV}}{(n - \Delta_{nl})^{2}}$$

其中 $\Delta_{nl}$ 被称为量子数亏损

碱金属光谱精细结构

以电子为参考系，原子核在绕着电子转动，这会产生一个磁场 $\overrightarrow{B}$，导致电子的自旋磁矩与之作用产生额外的势能：

$$E_s = -\mu\cdot\overrightarrow{B} = -\mu_{sz}B = \pm \mu_BB$$

这被称为自旋-轨道耦合能

由于这个能量的存在，确定了 $(n, l)$ 的能级会分裂出两个能级，分别对应 $m_s = \pm 1 / 2$ 的情况：

$$E_{nls} = E_{nl} \pm \mu_BB$$

也即对应两条谱线，由于自旋-轨道耦合能的绝对值很小，因此这两条谱线波长差很小，被称为精细结构

泡利不相容原理

微观粒子的全同性

在量子力学中，微观粒子运动状态用波函数描述，没有确定的轨道，是不可区分的，称为不可分辨性或全同性

假设一个系统拥有两个粒子，其波函数为 $\Psi(1, 2)$，则全同性要求：

$$|\Psi(1, 2)|^{2} = |\Psi(2, 1)|^2 \implies \Psi(1, 2) = \pm \Psi(2, 1)$$

即波函数必须是对称或者反对称的，直观上来理解是，对于包含了多个全同粒子的系统，交换任意两个全同粒子的状态之后，系统的可观测状态不会发生改变

我们考虑处在不同单粒子态状态 $A, B$ 的两个粒子 1, 2，则可以存在的系统状态是：

$$\Psi_\mathrm{I} = \Psi_A(1)\Psi_B(2),\quad \Psi_\mathrm{II} = \Psi_B(1)\Psi_A(2)$$

因此，为了满足对称性或者饭对称性，体系的波函数应该是上述两个状态按如下方式叠加后的结果：

$$\Psi(1, 2) = \frac{1}{\sqrt{2}}\left[\Psi_A(1)\Psi_B(2)\pm \Psi_B(1)\Psi_A(2)\right]$$

费米子与玻色子

首先，将自旋的概念从电子拓展到所有粒子，我们将自旋量子数 $s$ 为半整数的粒子称为费米子，$s$ 为整数的称为玻色子

费米子的波函数是反对称的，即：

$$\Psi(1, 2) = \frac{1}{\sqrt{2}}\left[\Psi_A(1)\Psi_B(2) - \Psi_B(1)\Psi_A(2)\right]$$

这说明当两个单粒子态相同，即 $A = B$ 时，$\Psi(1, 2) = 0$

这就是著名的泡利不相容原理：

而玻色子的波函数是对称的：

$$\Psi(1, 2) = \frac{1}{\sqrt{2}}\left[\Psi_A(1)\Psi_B(2) + \Psi_B(1)\Psi_A(2)\right]$$

因此多个玻色子可以占据同一单粒子态

原子核外电子排布

完备地描述原子中的电子的运动状态需要用一组量子数：

• 主量子数 $n \in \mathbb{N}^{+}$：决定能量的主要因素
• 角量子数 $l \in \{0,1,\dots,n-1\}$：决定能量的次要因素，对应同一层中的不同轨道 $s, p, d, f$
• 磁量子数 $m_l \in \{0,\pm 1,\dots,\pm(n-1)\}$：引起磁场中的能量分裂
• 自旋磁量子数 $m_s = \pm 1 / 2$：产生精细结构

根据泡利不相容原理，第 $n$ 层能容纳的电子数量为：

$$\sum\limits_{l = 0}^{n - 1}2(2l + 1) = 2n^2$$

而一般情况下，电子遵循能量最低原理，即优先填充能量较低的轨道，经验公式为，$(n + 0.7l)$ 越大，轨道能量越高

X 射线

X 射线发射谱

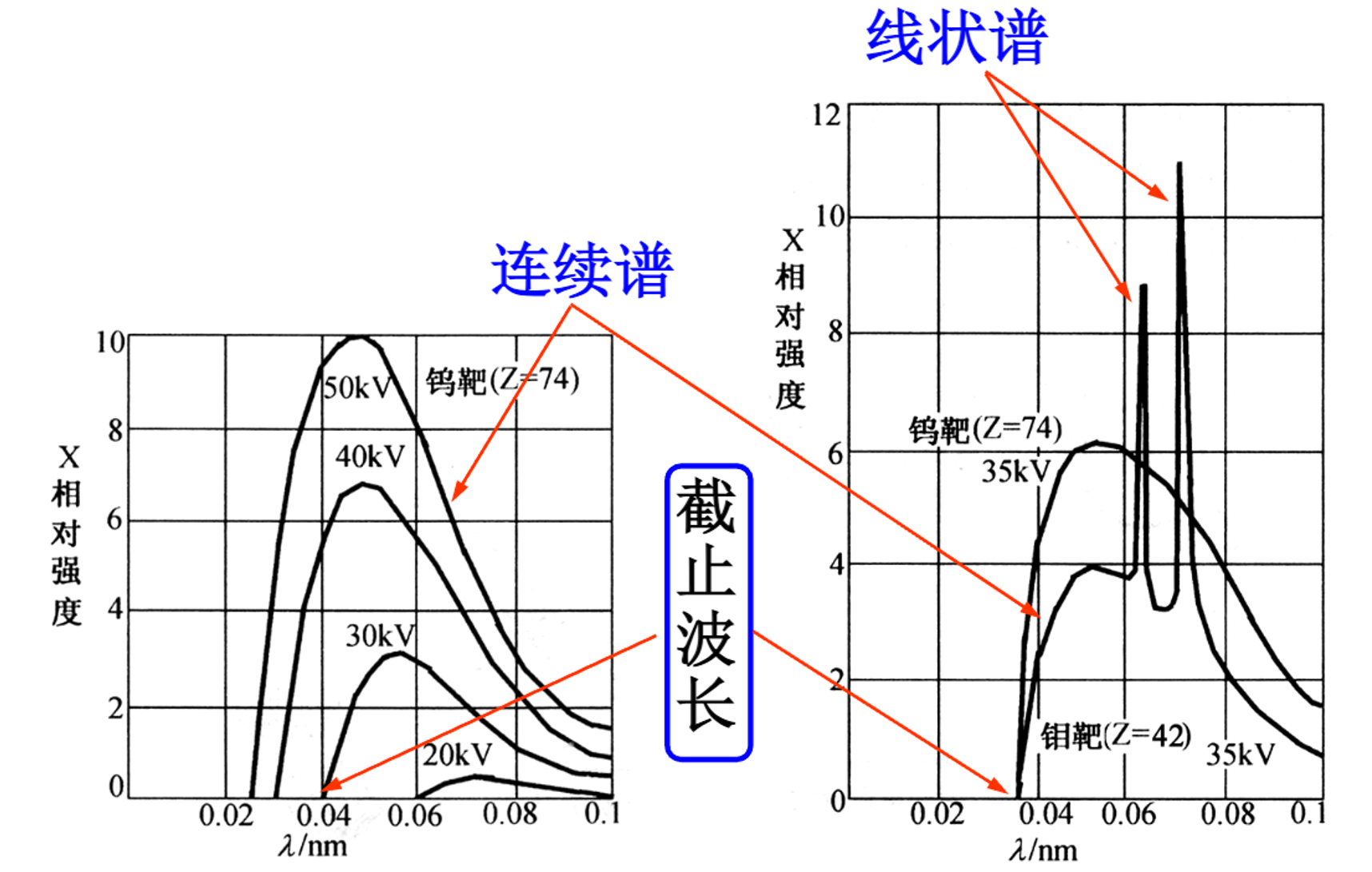
通过强电场加速热电子，轰击重金属靶可以得到 X 射线，其发射谱如上图所示

下面依次分析连续谱和线状谱

X 射线连续谱

连续谱起源于轫致辐射，也即在高速电子接近原子核时，库仑作用产生的负加速度降低了电子动能，而损失的能量以光子形式放出，辐射强度满足：

$$I \propto \left(\frac{Ze^2}{m}\right)^2$$

其中 $Z$ 为原子序数

由于每次射入时候产生的加速度是随机的，因此产生的是连续谱，而根据辐射强度表达式可以看出，其形状与靶材料无关，靶材料只会影响具体的辐射强度

根据能量守恒，所释放出的光子最大能量就是原电子的动能，因此存在截止波长：

$$eU = h\frac{c}{\lambda_{\min}} \implies \boxed{\lambda_{\min} = \frac{hc}{eU}}$$

这说明截止波长只与外加电压有关，与靶材料无关

X 射线线状谱

线状谱起源于电子的内层跃迁，其位置由元素决定，与外加电压 $U$ 无关

当高速电子将内层电子轰出，形成空位之后，外层的电子会跃迁到内层，产生辐射，从 $L, M, N, O \dots$ 跃迁到 $K$ 所释放的辐射分别记为 $K_\alpha, K_\beta, K_\gamma, K_\delta\dots$，以此类推

$K_\alpha$ 线频率满足莫塞莱定律：

激光

基本原理是受激辐射理论

原子的激发与辐射

自发辐射

激发态的原子自发跃迁到基态并且释放出光子的行为被称为自发辐射，这个过程是随机的，因此发射出的光是非相干光

令 $A_{21}$ 表示自发辐射系数，即单个原子在单位时间内发生自发辐射的概率，则 $E_2 \to E_1$自发辐射的原子数是：

$$\frac{\mathrm{d}N_{21}}{\mathrm{d}t} = A_{21} N_2 = -\frac{\mathrm{d}N_{2}}{\mathrm{d}t} = \frac{\mathrm{d}N_{1}}{\mathrm{d}t}$$

其中 $N_i$ 表示单位体积中处于能级 $E_i$ 的原子数

吸收

入射光子的能量恰好是能级差时，原子可能会吸收光子跃迁到高能级，则单位体积单位时间内，$E_1 \to E_2$ 跃迁的光子数为：

$$\frac{\mathrm{d}N_{12}}{\mathrm{d}t} = C_{12}\rho(\nu, T)N_1 = -\frac{\mathrm{d}N_{1}}{\mathrm{d}t} = \frac{\mathrm{d}N_{2}}{\mathrm{d}t}$$

其中 $C_{12}$ 是吸收系数，$\rho(\nu, T)$ 是温度为 $T$ 时，频率在 $\nu$ 附近，单位频率间隔内外来辐射场的能量密度

受激辐射

仅有自发辐射和吸收无法到达热平衡，需要通过受激辐射，即：

这说明受激辐射将原有的一个光子放大成了两个光子

单位体积单位时间内，$E_2 \to E_1$ 受激辐射的光子数为：

$$\frac{\mathrm{d}N_{21}}{\mathrm{d}t} = B_{21}\rho(\nu, T)N_2 = -\frac{\mathrm{d}N_{2}}{\mathrm{d}t} = \frac{\mathrm{d}N_{1}}{\mathrm{d}t}$$

其中 $B_{21}$ 是受激辐射系数

$A_{21}, B_{21}, C_{12}$ 统称为爱因斯坦系数，其满足：

$$B_{21} = C_{12},\quad A_{21} = \frac{8\pi h\nu^3}{c^3}B_{21}$$

布居反转

由大量原子组成的系统，在温度不太低的平衡态，原子数目按能级的分布服从玻耳兹曼统计分布，即 $E_n$ 能级的粒子数满足：

$$N_n \propto \exp\left(-\frac{E_n}{kT}\right)$$

这说明 $N_2 < N_1$

而当入射光子能量为 $h\nu = E_2 - E_1$ 的时候，如果想让系统整体产生光放大，需要满足：

$$C_{12}\rho(\nu, T)N_1 < B_{21}\rho(\nu, T)N_2 \implies N_1 < N_2$$

这说明产生光放大必须在非热平衡态