大学物理 磁力与磁场

Chapter 6 - 磁场与磁力

磁力的规律

电荷在磁场中受力

\overrightarrow{F} = q\vec{v}\times\vec{B}

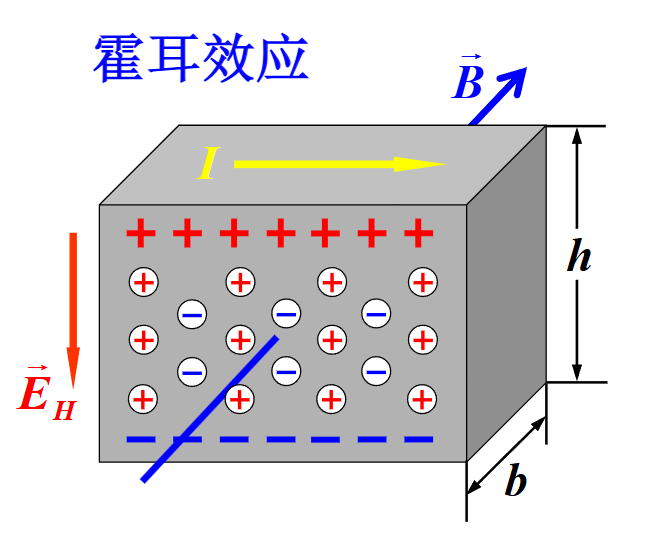
霍尔效应示意图

当电流垂直于外磁场通过导体时，载流子发生偏转，垂直于电流和磁场的方向会产生一附加电场，从而在导体的两端产生电势差

q_0E_H = q_0vB = q_0 \frac{I}{nqS}B \implies E_H \frac{IB}{nqS}

其中 $S = hb$ 为材料横截面积， $q$ 为载流子电荷

因此霍尔电势差为：

U_H = E_H h = \frac{IB}{nbq}

定义 $K_H = \dfrac{1}{nq}$ 为霍尔系数，只与材料有关

电流元在磁场中受力：

d\overrightarrow{F} = I \mathrm{d}\vec{l}\times\vec{B} \implies \overrightarrow{F} = \int\limits_{L} I \mathrm{d}\vec{l}\times\vec{B}

安培力大小为：

F = IlB \sin\theta

对于在均匀外磁场中的载流线圈，将其类比成均匀外电场中的电偶极子，定义磁矩为：

\vec{m} = I \overrightarrow{S}

其中 $\overrightarrow{S}$ 的方向由电流根据右手螺旋确定

则其力矩和势能分别为：

\begin{align*} \overrightarrow{M} &= \vec{m}\times\overrightarrow{B} \\ W &= -\vec{m}\cdot\overrightarrow{B} \end{align*}

某一电流元 $I\mathrm{d}\vec{l}$ 在某一点 P 处产生的磁场为：

\mathrm{d}\overrightarrow{B} = \frac{\mu_0}{4\pi}\frac{I\mathrm{d}\vec{l}\times\vec{e}_r}{r^2}

其中， $\vec{e}_r$ 是该电流元指向 $P$ 点的单位方向向量， $\mu_0$ 为真空磁导率，定义为：

\mu_0 = \frac{1}{\varepsilon_0 c^2} = 4\pi \times 10 ^{-7} \,\,\rm T·m/A

右手螺旋！

同样磁场也有叠加原理，例如可以证明，载流线圈中心轴线上的磁感应强度大小为：

B = \frac{\mu_0 I S}{2\pi(R^2 + x^2)^{3/2}}

根据安培力公式和 BS 定律推导而来，适用于两孤立电流元之间的力：

\begin{align*} \mathrm{d}\overrightarrow{F}_{12} &= I_2\mathrm{d}\vec{l}_2\times\left(\frac{\mu_0 I_1\mathrm{d}\vec{l}_1\times \vec{r}_{12}}{4\pi r_{12}^3}\right) \\ \mathrm{d}\overrightarrow{F}_{21} &= I_2\mathrm{d}\vec{l}_1\times\left(\frac{\mu_0 I_2\mathrm{d}\vec{l}_2\times \vec{r}_{21}}{4\pi r_{21}^3}\right) \end{align*}

一般情况下，孤立电流元的相互作用力不满足牛顿第三定律，但这个系统仍然满足动量守恒，场源（电荷、电流元等）的动量与所激发的场的动量是守恒的

也称为磁通连续原理

定义任一曲面 $S$ 的磁通量：

\varPhi = \iint\limits_S \overrightarrow{B}\cdot\mathrm{d}\vec{s}

则该定理表示任何磁场中通过任意封闭曲面的磁通量为 0，即：

\oiint\limits_S \overrightarrow{B}\cdot\mathrm{d}\vec{s} = 0

根据高斯公式可以得到其微分形式为：

\nabla \cdot \overrightarrow{B} = 0

表示磁感应强度的环路积分应该正比于这个路径所包围的电流强度代数和，即：

\oint\limits_L\overrightarrow{B}\cdot\mathrm{d}\vec{l} = \mu_0\sum I_{\text{in}}

其中符合右手螺旋定则方向的电流为正