大学物理 电磁感应

Chapter 8 - 电磁感应

法拉第电磁感应定律

定义磁通链 $\Psi$ 为通过一个 $N$ 匝线圈每一匝的磁通量之和，对于一个均匀长直螺线管，有：

$$\Psi = N\Phi$$

对于 $N$ 匝的线圈，磁通量发生改变的时候产生的感应电动势为：

$$\mathscr{E} = -\frac{\mathrm{d}\Psi}{\mathrm{d}t} = -N\frac{\mathrm{d}\Phi}{\mathrm{d}t}$$

当回路中存在电阻的时候，感应电流为：

$$I = -\frac{N}{R}\cdot\frac{\mathrm{d}\Phi}{\mathrm{d}t}$$

楞次定律！

来拒去留！

动生电动势

线圈动导致磁通量变化

若线圈在以 $\overrightarrow{V}$ 运动，则产生的动生电动势为：

$$\mathscr{E} = \oint_L \left(\overrightarrow{V}\times\overrightarrow{B}\right)\cdot\mathrm{d}\vec{l}$$

得到：

$$\mathrm{d}\mathscr{E} = \left(\overrightarrow{V}\times\overrightarrow{B}\right)\cdot\mathrm{d}\vec{l}$$

动生电动势的本质是：载流子随导线一起运动收到的洛伦兹力，作为非静电性场强产生的电动势

电动势的方向由右手定则确定

能量关系

动生电动势电功率：

$$\mathrm{d}P_e = I \mathrm{d}\mathscr{E} = I \left(\overrightarrow{V}\times\overrightarrow{B}\right)\cdot\mathrm{d}\vec{l}$$

而导体运动受到安培力的功率为：

$$\mathrm{d}P_a = \mathrm{d}F\times \overrightarrow{V} = I \left(\mathrm{d}\vec{l}\times\overrightarrow{B}\right)\cdot\overrightarrow{V}= -I \left(\overrightarrow{V}\times\overrightarrow{B}\right)\cdot\mathrm{d}\vec{l}$$

这说明了总功率为零，而这两个力的微观本质都是洛伦兹力，因此对应了洛伦兹力不做功

感生电动势

容易得到：

$$\mathscr{E}_{\text{感}} = -\iint\limits_{S}\frac{\partial \overrightarrow{B}}{\partial t}\cdot\mathrm{d}\vec{s}$$

其中 $\mathrm{d}\vec{s}$ 的正向由线圈绕向根据右手定则确定

感生电场

变化的磁场可激发一种新的非静电性质的场，称为感生电场，是产生感生电动势的根源，场强满足：

$$\oint_L\overrightarrow{E}_{\text{感}}\cdot\mathrm{d}\vec{l} = -\iint\limits_{S}\frac{\partial \overrightarrow{B}}{\partial t}\cdot\mathrm{d}\vec{s}$$

这实际上是感生电场的安培环路定理

与常见的静电场不同，感生电场是非保守场，电场线是围绕着 $\overrightarrow{B}$ 的闭合曲线

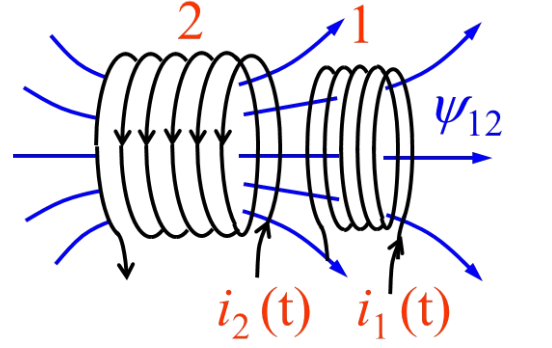
互感

一个线圈的电流发生变化时，其周围的导体回路中会出现感生电动势，被称为互感

互感示意图

考虑上图模型，假设回路 $a$ 的磁场，通过回路 $b$ 的磁通链为 $\Psi_{ba}$，则：

$$\Psi_{ba} = M i_a, \quad \{a, b\} = \{1, 2\}$$

其中 $M$ 为互感系数，由两线圈大小、形状、圈数、相对位形和介质情况决定，单位为亨利

因此线圈 $b$ 产生的互感电动势为：

$$\mathscr{E}_{ab} = -M\frac{di_b}{dt}$$

自感

对于一个电流回路，其磁通链和电流之间满足：

$$\Psi = Li$$

$L > 0$ 为自感系数，由线圈数、形状、尺寸和介质情况等因素决定，$\Phi$ 的正向与 $i$ 的正向成右手螺旋关系

自感电动势为：

$$\mathscr{E}_L = -L\frac{di}{dt}$$

对于填充了磁介质的长直螺线管，有：

$$B = \mu_rB_0 \approx \mu_r\mu_0 nI = \mu n I \implies \Phi = NBS \approx nl\cdot\mu n I \cdot S$$

因此：

$$L = \frac{\Phi}{I} \approx \mu n^2 lS$$

磁场能量

类比电容存储了静电能，电感也存储了磁能，公式为：

$$W_m = \frac{1}{2}LI^2$$

对于体积为 $V$ 的螺线管，有：

$$W_m = \frac{1}{2}\mu n^2 lS I^2 = \frac{B^2}{2\mu} V$$

因此磁能密度为：

$$w_m = \frac{W_m}{V} = \frac{B^2}{2\mu} = \frac{1}{2}BH$$

这个公式可以扩展为除铁磁质外的一切线性磁介质：

$$w_m = \frac{1}{2}\overrightarrow{B}\cdot\overrightarrow{H}$$

因此对于一般的系统，可以计算其储存的磁能为：

$$W_m = \iiint w_m \mathrm{d}V$$