大学物理 电介质

Chapter 4 - 静电场中的电介质

电介质的极化

电介质不导电，极化是指电介质在电场作用下，体内或界面出现极化电荷（束缚电荷）的现象

极化机制

1. 无极分子的位移极化：指没有极性的分子，在外电场作用下，电子云产生畸变，产生感生电偶极矩，电介质端面出现极化电荷
2. 有极分子的取向极化：有极性的分子，在外电场作用下，固有电偶极矩受热运动的影响，只能尽量沿外场方向排列，介质可呈现电性，电介质端面出现束缚电荷

极化强度

定义为单位体积中分子电偶极矩的矢量和，即：

$$\overrightarrow{P} = \frac{\sum\overrightarrow{p}}{\Delta V}$$

电介质的极化规律

当 $\overrightarrow{E}$ 不太强的时候，可以认为 $\overrightarrow{P}\propto \overrightarrow{E}$，称为线性电介质

对于各向同性的线性电介质来说，有：

$$\overrightarrow{P} = \varepsilon_0\chi_e\overrightarrow{E} = \varepsilon_0(\varepsilon_r - 1)\overrightarrow{E}$$

其中，$\chi_e$ 称为电极化率，$\varepsilon_r$ 称为相对介电常量

对于各向异性的线性电介质来说，有：

$$\overrightarrow{P} = \varepsilon_0\Chi_e\overrightarrow{E}$$

展开为矩阵形式为：

$$\begin{pmatrix} P_x \\[1em] P_y \\[1em] P_z \end{pmatrix} = \varepsilon_0 \begin{bmatrix} (\chi_e)_{xx}, (\chi_e)_{xy}, (\chi_e)_{xz} \\[1em] (\chi_e)_{yx}, (\chi_e)_{yy}, (\chi_e)_{yz} \\[1em] (\chi_e)_{zx}, (\chi_e)_{zy}, (\chi_e)_{zz} \end{bmatrix} \begin{pmatrix} E_x \\[1em] E_y \\[1em] E_z \end{pmatrix}$$

极化电荷

对于任一封闭曲面 $S$，其包围的极化电荷量为：

$$q_{\text{in}}' = -\oiint\limits_{S}\overrightarrow{P}\cdot\,\mathrm{d}\vec{s}$$

利用高斯定理，可推导出其体电荷密度为：

$$\rho' = -\nabla \cdot \overrightarrow{P}$$

在介质和真空交界面处的极化面电荷密度可以证明为：

$$\sigma' = \overrightarrow{P}\cdot\vec{e}_n$$

其中 $\vec{e}_n$ 的方向是由介质指向真空

有介质时的静电场规律

有介质时，高斯定理和环路定理仍然成立，但是由于极化电荷量并不已知，所以直接使用原始的高斯定理并不方便，因此代入极化电荷量的表达式可得：

$$\oiint\limits_{S} (\varepsilon_0\overrightarrow{E} + \overrightarrow{P})\cdot\mathrm{d}\vec{s} = \sum{q_{0\text{ in}}}$$

定义电位移矢量：

$$\overrightarrow{D} = \varepsilon_0\overrightarrow{E} + \overrightarrow{P}$$

则得到 $\overrightarrow{D}$ 的高斯定理：

$$\oiint\limits_{S} \overrightarrow{D}\cdot\mathrm{d}\vec{s} = \sum{q_{0\text{ in}}}$$

利用高斯定理得到微分形式为：

各向同性线性电介质

代入 $\overrightarrow{D}$ 的表达式，可以得到：

$$\begin{align*} \overrightarrow{P} &= \left(1 - \frac{1}{\varepsilon_r}\right)\overrightarrow{D} \\ \overrightarrow{D} &= \varepsilon_0\varepsilon_r\overrightarrow{E} \end{align*}$$

定义 $\varepsilon = \varepsilon_0\varepsilon_r$，称为电容率（介电常数）

并且在均匀各向同性的介质中，可以证明，体内自由电荷为零的地方，极化电荷也必然为零

考虑半径 $R_1$，带电 $q_0$ 的导体球，套均匀介质球壳，外半径 $R_2$，相对介电常量 $\varepsilon_r$，则可以证明其电场分布为：

$$\overrightarrow{E}(r) = \begin{cases} 0 & r < R_1 \\[1em] \dfrac{q_0}{4\pi\varepsilon_0\varepsilon_r r^2} \vec{e}_r & R_1 < r < R_2 \\[1em] \dfrac{q_0}{4\pi\varepsilon_0 r^2} \vec{e}_r & r > R_2 \end{cases}$$

在真空中，$\varepsilon_r = 1$，因此 $\overrightarrow{P} \equiv \mathbf{0}$

静电场的界面关系

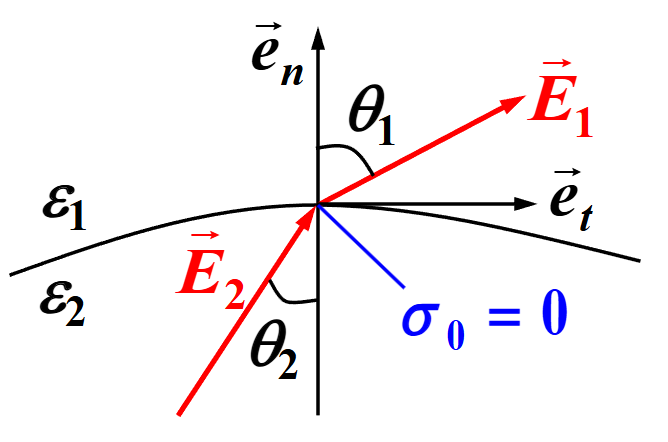
考虑两种介质被一个无限大平面分隔开，二者介电常数分别为 $\varepsilon_1, \varepsilon_2$，此时分界面上电场满足什么条件呢，设分界面电荷密度为 $\sigma_0$，可以证明：

1. 法向关系：

$$\left(\overrightarrow{D}_1 - \overrightarrow{D_2}\right)\cdot \vec{e}_n = \sigma_0$$

其中 $\vec{e}_n$ 由介质 2 指向介质 1

2. 切向关系：

$$\overrightarrow{E}_1 \cdot \vec{e}_t= \overrightarrow{E}_2 \cdot \vec{e}_t$$

其中 $\vec{e}_t$ 沿分界面切向

3. 对于各项同性介质，若 $\sigma_0 = 0$，可以由几何关系得到：

$$\frac{\tan \theta_1}{\tan\theta_2} = \frac{\varepsilon_1}{\varepsilon_2}$$

电场线形成了类似光线的折射

电容

对于孤立带电导体，可以证明 $\dfrac{Q}{U} \equiv \text{const}$，若使用金属壳进行静电屏蔽，就得到了电容器

常见电容器的电容是：

带介质的静电场能量

定义电容器存储的能量是指使电容器带电外界所做的功，可以证明：

$$W = \frac{Q^2}{2C} = \frac{1}{2}CU^2 = \frac{1}{2}QU$$

对于平行板电容器：

$$W = \frac{1}{2}\frac{\varepsilon S}{d}(Ed)^2 = \frac{1}{2}\varepsilon E^2 (Sd)$$

因此可以定义能量密度：

$$w_e = \frac{W}{Sd} = \frac{1}{2}\varepsilon E^2 = \frac{1}{2}E D$$

这个公式可以推广，即对于任意线性介质：

$$w_e = \frac{1}{2}\overrightarrow{E}\cdot\overrightarrow{D}$$