Chapter 1 - 静电场
主要涉及电荷、库仑定律、高斯定理等
电荷守恒定律
e=1.602176565×10−19C
电量是相对论不变量(运动不改变物体电荷)
库仑定律
描述真空点电荷相互作用,要求施力电荷对观测者静止
基本形式:
F12=kr212q1q2er21=−F21
其中 k=9×109N⋅m2/C2
将其有理化,引入真空介电常数
ε0=4πk1=8.85×10−12C2/(N⋅m2)
则:
F12=4πε0r212q1q2er21=−F21
电场与电场强度
根据静止检验电荷所受电场力定义:
E=q0F
场强叠加原理:
点电荷系产生的总场强等于每个点单独存在时产生的场强的叠加
常见静电场场强
点电荷与点电荷系
源电荷 q 距离 r 处场点的场强为:
E=4πε0r2qer∝r21
由场强叠加原理可得点电荷系的场强:
E=i∑4πε0ri2qieri
电偶极子
一对靠得很近的等量异号点电荷构成的点电荷系,中点为 O, 二者的位矢为 l,定义场点距离为场点 P 到点 O 的距离,当场点距离 r>>l 时可以视为电偶极子
我们定义电偶极矩 p=ql,用于描述电偶极子的强度与方向
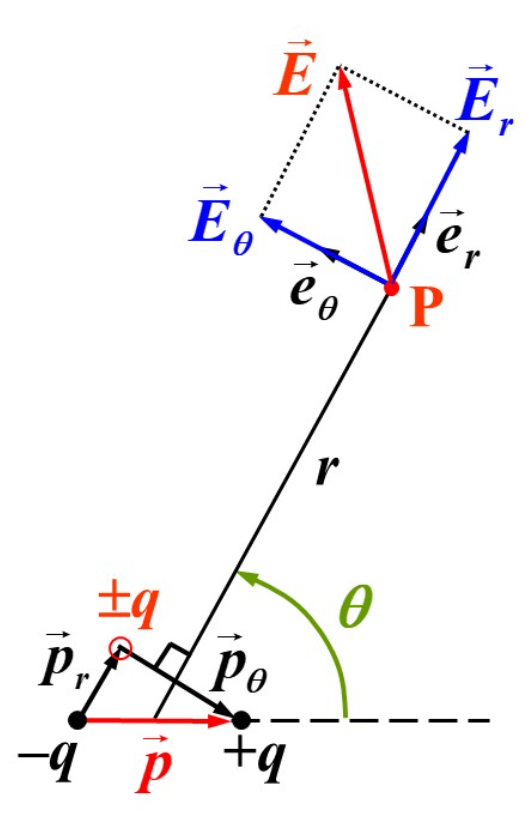
可以推导处,对于任意点 P,若 OP 与 p 的夹角为 θ,则 P 处场强为:
E=4πε0r31(r23(r⋅p)r−p)∝r31
证明过程如下
证明过程
我们将电偶极矩 p 进行正交分解,以 OP 为径向,这样我们可以分别计算径向和切向的场强,在进行叠加
首先考虑对于电偶极矩 p,其轴线上场点距离为 r 的点处的场强:
E=E++E−=4πε0qel[(r−2l)21−(r+2l)21]=4πε0r2qel[(1−2rl)−2−(1+2rl)−2]≈4πε0r2qel(1+rl−(1−rl))=2πε0r3ql=2πε0r3p
其中近似是因为 l/r→0
接下来证明中垂线上的场强,根据几何关系可以得到场强方向应该与 p 相反
E=E++E−=4πε0(r2+(2l)2)1(qer+−qer−)≈4πε0r2q(er+−er−)=4πε0r3q(r+−r−)=−4πε0r3ql=−4πε0r3p
因此对于一般情况,将其正交分解后进行叠加:
$$\begin{align*} \overrightarrow{E} &= \overrightarrow{E}_r + \overrightarrow{E}_\theta = \frac{\overrightarrow{p}_r}{2\pi\varepsilon_0r^3} - \frac{\overrightarrow{p}_\theta}{4\pi\varepsilon_0r^3} \\ &= \frac{1}{4\pi\varepsilon_0r^3}(2\overrightarrow{p}_r - \overrightarrow{p}_\theta) \\ &= \frac{1}{4\pi\varepsilon_0r^3}(3\overrightarrow{p}_r - \overrightarrow{p}) \\ &= \frac{1}{4\pi\varepsilon_0r^3}\Big(\frac{3(\overrightarrow{r}\cdot\overrightarrow{p})\overrightarrow{r}}{r^2} - \overrightarrow{p}\Big)\end{align*}$$证毕
在均匀外电场中,可以证明电偶极子所受力矩为:
M=p×E
即会使电偶极子的空间取向尽量与外电场一致
连续带电体
将带电体分割成无限多的小电荷元
E=∫dE=q∫4πε0r2erdq
通常,体电荷密度记为 ρ,面电荷密度记为 σ,线电荷密度记为 λ
一道例题
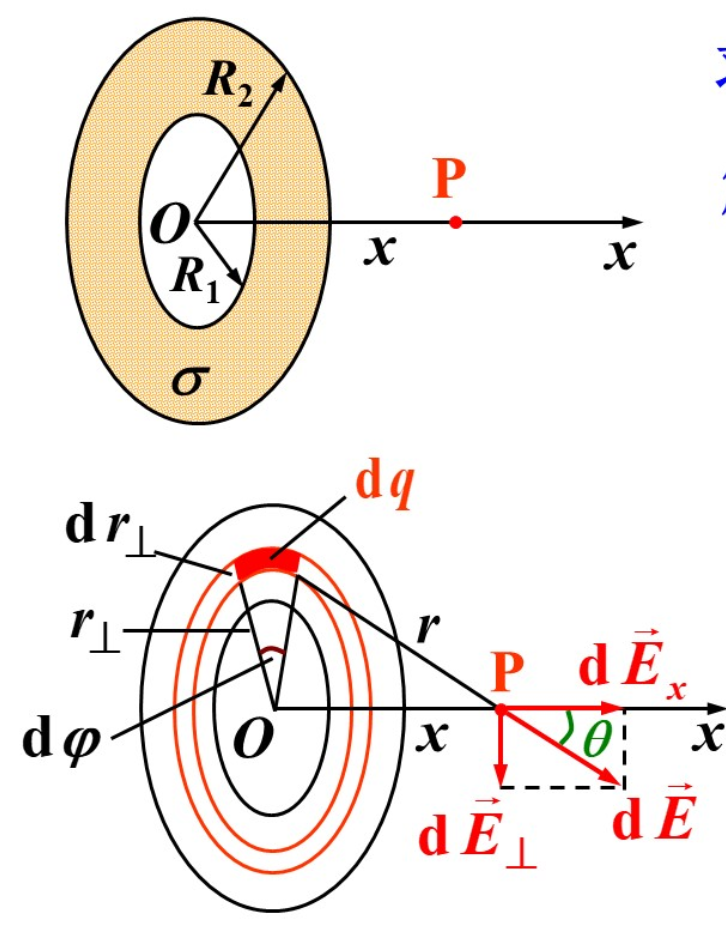
一均匀带电环面,面电荷密度 σ,内外径 R1,R2,求其轴线上距离圆环中心 x 处的场强 E
如上图,在环面上任取电荷元 dq,其方位角为 φ∈[0,2π],与环面中心的距离为 r⊥,则其面积为:
ds=r⊥dr⊥dφ
则:
dE=4πε0r2erdq
将其按照轴线和环面方向作正交分解,得到 dE=dEx+dE⊥
由于 φ 的对称性,可以证明:
∫dE⊥=0
因此:
E=∫dE=∫dEx=∫4πε0r2er⋅rxdq=∫02π∫R1R24πε0r3xσr⊥erdr⊥dφ=er⋅2ε0xσ∫R1R2r3r⊥dr⊥=er⋅2ε0xσ∫R1R2(x2+r⊥2)3r⊥dr⊥=er⋅2ε0xσ(−x2+r⊥21)R1R2=er⋅2ε0xσ(x2+R121−x2+R221)
当 R1→0,R2→∞ 时,有:
E=er⋅2ε0σ
这解释无限大均匀带电平面两侧的场强,可以看出这是一个匀强电场,平面两侧方向相反
电场线与电通量
电场线用于描述场强:
- 每一点的切向为场强方向
- 数密度描述了场强大小:E=dN/dS⊥
电通量定义为:
Φe=S∬Eds
高斯定理
静电场中,通过任意一个闭合曲面 S 的电通量 Φe,等于该曲面所包围的电量的代数和 ∑qin 除以 ε0
Φe=S∬Eds=ε0∑qin